函数的零点问题VIP免费

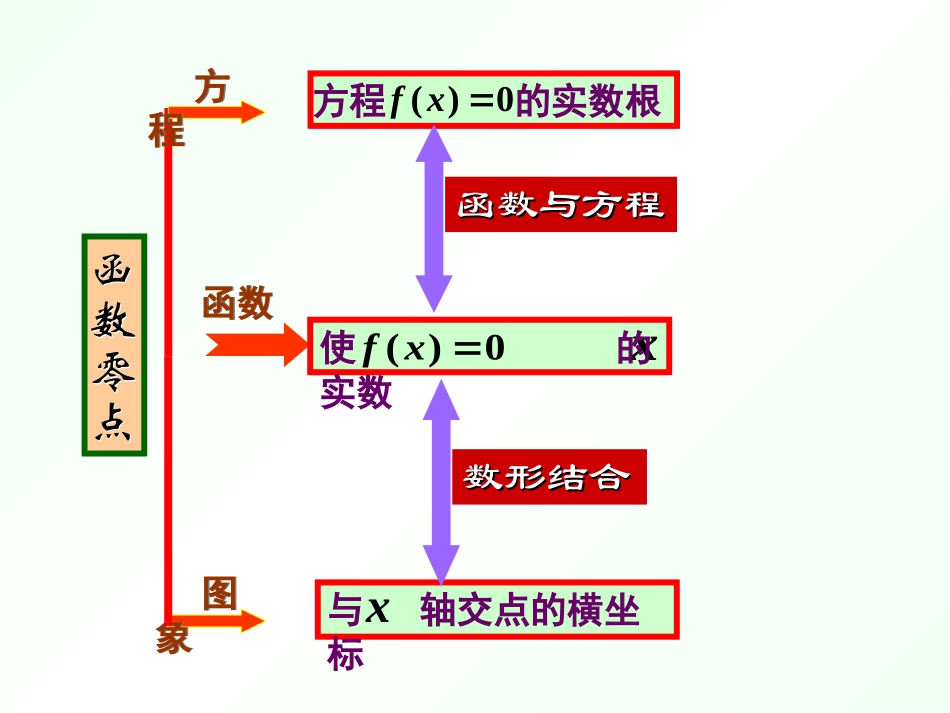
函数的零点问题函数零点是新课标教材的新增内容之一,纵观近几年全国各地的高考试题,经常出现一些与零点有关的问题,它可以以选择题、填空题的形式出现，也可以在解答题中与其它知识交汇后闪亮登场，可以说”零点”成为了高考新的热点、亮点和生长点.高考地位方程方程0)(xf方程的实数根与轴交点的横坐标x函数与方程函数与方程函数与方程函数与方程数形结合数形结合数形结合数形结合函数函数0)(xfx使的实数函数零点函数零点图象图象唯一)(xf在ba,上单调0)()(bfaf)(xf在有ba,零点)(xf在ba,上连续零点的存在性定理一、直接求函数的零点求根定零点[例1](2012湖北)函数在区间[0，4]上的零点的个数为()2()cosfxxxA.4B.5C.6D.7C22()cos00cos0fxxxxx或0,.2xxkk或2Z00,2.0,1,2,324kxxk或[B可以是（）[练习]若函数的零点与之差的绝对值不超过0.25，则C.D.)(xf224)(xxgx的零点)(xfA.B.14)(xxf2)1()(xxf1)(xexf)21ln()(xxfA二、确定零点的大致位置异号定零点位置()()0fbfc()()0fafbA三、求零点的个数画图定零点个数A三、求零点的个数xxfy21)([练习]定义在R上的奇函数，当时，且当时，有求函数的零点个数。10x,2)(1xxf1x)1()(xfxf)(xf1234125oxy画图定零点个数四、根据零点探参数用图定参数5(1,)4四、根据零点探参数用图定参数有两个零点，求实数的已知函数lnx,g(x),)(2xaxxf[练习])()()(xgxfxh的取值范围。a若函数2lnxxxa32ln21)ln(xxxxxxay1oxy1五、综合应用[例5]确定函数1096)(23xxxxf零点的个数x)1,(1(1,3)3),3(/y+0-0+y增函数Y极大值-6减函数Y极小值-10增函数-10XXYO13-6解：1096)(23xxxxf，)3)(1(39123)(2/xxxxxf令0)(xf,得3,121xx列出x,y/,y的对应值表如下：x)1,(1(1,3)3),3(/y+0-0+y增函数Y极大值-6减函数Y极小值-10增函数作出函数的1096)(23xxxxf草图可知，函数)(xf的图象与X轴仅有一个交点，则)(xf仅有一个零点。注意：本类型题的特点是找出函数)(xf的图象与X轴交点的情况，-10XYO13变式一（引入参数a）试讨论函数axxxxf1096)(23(Ra)零点的个数。想一想，下面的题如何解？变式一：试讨论函数axxxxf1096)(23(Ra)零点的个数。分析：方法1：.直接模仿上面的解法，可得如与表格:x)1,(1(1,3)3),3(/y+0-0+y增函数ay极大值6减函数ay极小值10增函数然后再结合函数)(xf的图象与X轴的关系，确定分类讨论的标准，讨论极大值、极小值与零的关系，讨论图象与X轴交点情况，得出如下结论：当010ay极小值即10a时没有1个交点；当010ay极小值即10a时仅有2个交点；当010ay极小值且06ay极大值即610a时有3个交点；当即06ay极大值6a时有2个交点；当06ay极大值即6a时有1个交点.方法2：构造函数1096)(23xxxxf与axg)(，利用前面的方法可得到函数)(xfy的图象，从两个函数图象的位置关系，可得：当)10,(a仅有1个零点；当10a有2个零点；当)6,10(a有3个零点；当6a时有2个零点；当),6(a仅有一个零点。-10)(xfyXYO13-6-10XXYO13-6变式二（方程问题）若方程axxx109623在]31[，上有实数解，求a的取值范围。610a变式三（改变参数的位置）若方程0923xaxx在[1，3]上有实数解，求a的取值范围。]10,6[a]3,1[,9923xxxxxxa思考：如何转化？方法一方法二方程092axx在[1，3]上有实数解变式四（把相等关系变成不等关系）若不等式0923xaxx在[1，3]上恒成立，求a的取值范围。]6,(a分析：转化为]3,1[,9xxxa恒成立问题，即]3,1[,)9(minxxxa小结提炼函数零点函数方程数形结合思想分类讨论知识是根，思想是干类题是枝，个题是叶零数零位零点零参（天津）已知函数（1）求函数f（x）的单调区间；（2）若函数f（x）在区间（-2，0）内恰有两个零点，求a的取值范围；3211(),,0.32afxxxaxaxRa其中(1)()---1fxa的增区间是（，1），（a,+);单调递减区间是（，）.(2)(2)0(1)01(0)0,03fffa解得的取值范围是（，）.课后作业：数学中的一些美丽定理具有这样的特性：它们极易从事实中归纳出来，但证明却隐藏的极深。——高斯