正切函数的性质与图像VIP免费

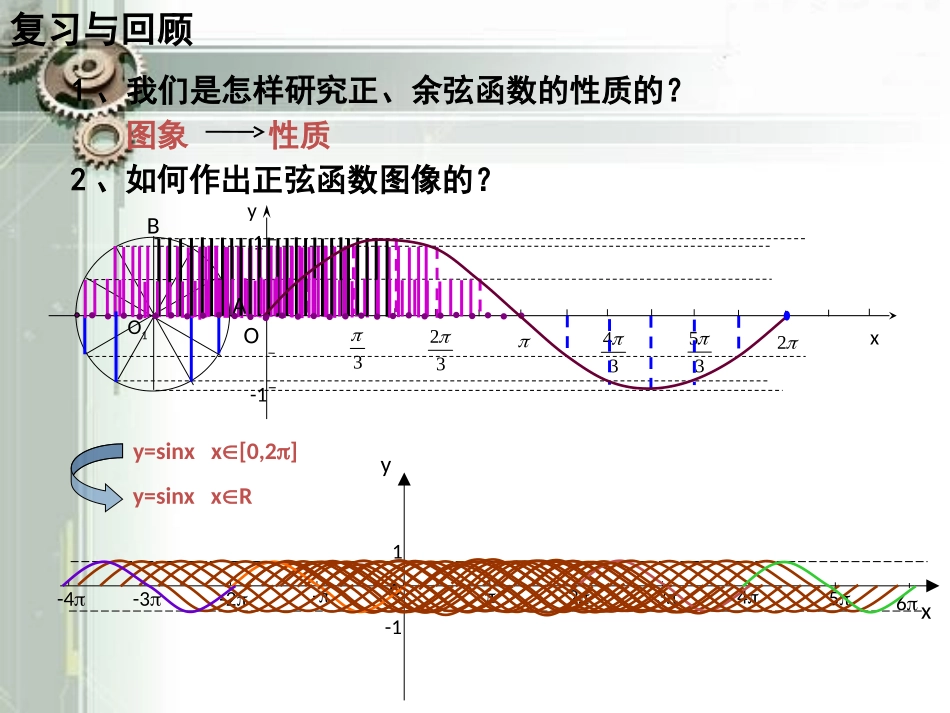
正切函数的性质与图像复习与回顾1、我们是怎样研究正、余弦函数的性质的？图象性质2、如何作出正弦函数图像的？O1Oyx33234352-11ABx6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正切函数的性质1、定义域Zkkxx,2|2、周期性tan()tanxx可知，正切函数是周期函数，且周期为ATxOyxytan3、奇偶性思考：定义域Zkkxx,2|是否关于原点对称？由tan()tanxx因而tan,,2yxxkkZ是奇函数。AT1T2xOyTATATxOyxOyxyAATxOyO4、单调性xyO1234T4T3T2T1A如图，在121212tantanATAT即因而tany在(0,)2单调递增；在(,0)2内434343tantanATAT即因而tany在(,0)2单调递增；所以tany(,)22单调递增(0,)2内在综上(,)22是tany的一个单调递增区间。又周期为所以tany在每一个开区间(,),22kkkZ单调递增，无单调递减区间。0,kzkk且5、值域由正切线可以看到，tan(,)22x在内可以取任意实数，但没有最大值、最小值因此，正切函数的值域是实数集RxyO正切函数的图象22XXYY22323正切曲线图像特征：正切曲线是被互相平行的直线,2xkkZ所隔开的无穷多支曲线组成的。在每一个开区间(,),22kkkZ内，图像自左向右呈上升趋势，向上与直线,2xkkZ无限接近但,2xkkZ无限接近但永不请同学们从正切函数图像出发，验证其性质。永不相交；向下与直线相交。2、将,2xkkZ称为正切曲线的渐近线。1、间断性：例1、求函数y=tan()的定义域、周期和单调区间23x例2、不求值，比较下列函数值大小：(1)tan138tan1431317(2)tan(-)tan(-)45与与R22kk，ZkZk2kx奇函数{2Z}xxkk，定义域值域周期奇偶性单调增区间渐近线方程xytan（1）的作图是利用平移正切线得到的，当我们获得上图像后，再利用周期性把该段图像向左右延伸、平移。22，小结：（2）性质:（3）思想方法：类比、推理、转化