反比例函数的图象及性质VIP免费

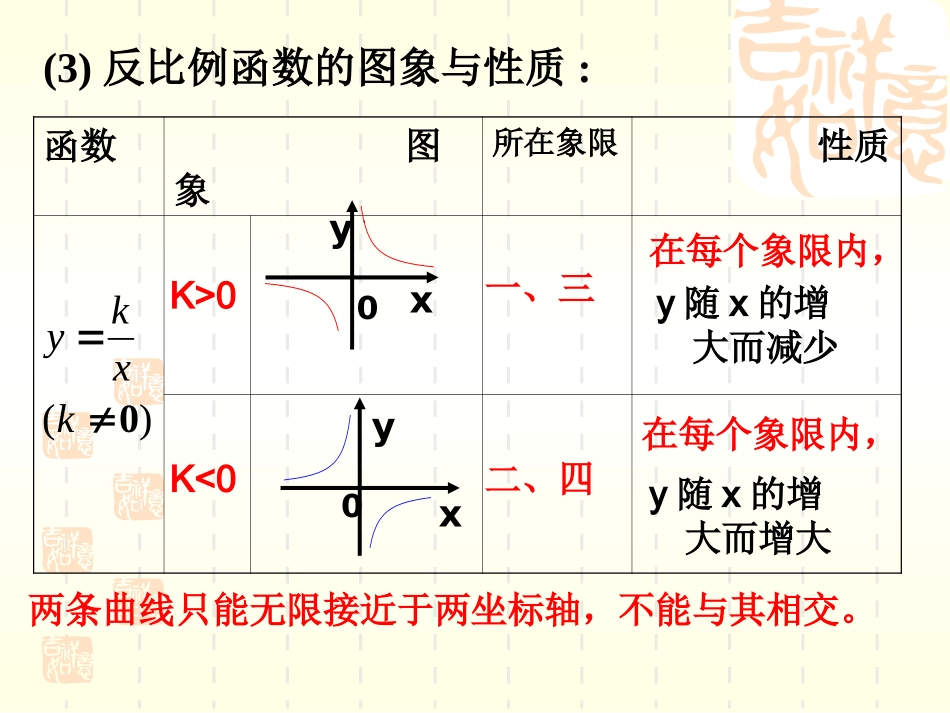
反比例函数图象和性质复习回顾（1）反比例函数的图像的形状是；并且与x、y轴没有；（2）反比例函数的图像与两坐标轴的距离由决定，，图像离坐标轴越近，，图像离坐标轴越远。双曲线交点kk越小k越大(3)反比例函数的图象与性质:函数图象所在象限性质)(0kxkyK>0K<0y0xyx0一、三二、四在每个象限内，y随x的增大而减少在每个象限内，y随x的增大而增大两条曲线只能无限接近于两坐标轴，不能与其相交。1.如果反比例函数y=的图像过点P(-2，3)，那么k的值是.2.反比例数当x>0时,y随x的增大而增大,则m=.3.如果反比例函数的图象位于第二、四象限，那么m的范围为.夯实基础xk2212mxmy)(x3m1y-6-131mK=xy=-2×3=-6 m2-2=-1m=±12m-1<0m=-1∴ ∴ 1-3m<0m>∴31yy332.则面积为S,ΔABC的,B平行于x轴,轴AC平行于y的任意两点,像上关于原点O对称的图x1B是函数yA,5.如图,ACoyxBCDEBC如图是反比例函数的图象一支，根据图象回答下列问题：（1）图象的另一支在哪个象限？常数m的取值范围是什么？5myx例1（2）在这个函数图象的上任取点A(a，b)和B(a′,b′)，如果a>a′，那么b和b′有怎样的大小关系？例2金P35-14题例2金P35-15题如图,在平面直角坐标系中,函数(x>0,m是常数)的图象经过A(1,4)、B（a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD、DC、CB。（1）若△ABD的面积为4，求点B的坐标；（2）求证：DC∥AB；（3）当AD=BC时，求直线AB的解析式。提升能力xmyOyX●A(1,4)●B(a,b)CD如图,在平面直角坐标系中,函数(x>0,m是常数)的图象经过A(1,4)、B（a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD、DC、CB。（1）若△ABD的面积为4，求点B的坐标；提升能力OyX●A(1,4)●B(a,b)CDxmy∴m=1×4=4设BD与AC交于E点.∴点B的坐标为(3,)34∴DB=a,AE=4-a4依题意得:B点的坐标为(a,)D点的坐标为(0,)E点的坐标为(1,)a4a4a4解: 函数的图象经过A(1,4)xmy∴SABD△=BD·AE=a·(4-)=4,得a=32121a4E提升能力如图,在平面直角坐标系中,函数(x>0,m是常数)的图象经过A(1,4)、B（a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD、DC、CB。（1）若△ABD的面积为4，求点B的坐标（2）求证:DC∥AB；xmyOyX●A(1,4)●B(a,b)CDE∴DE=1,BE=a-1,AE=4-,CE=a4a4证明:(2)由题意得:C(1,0),B(a,)E(1,),D(0,)a4a4a4∴1aa4a44CEAE1,aDEBE又 ∠AEB=CED∠∴△AEBCED∽△∴∠BAE=DCE∠∴DCAB∥CEAEDEBE∴提升能力如图,在平面直角坐标系中,函数(x>0,m是常数)的图象经过A(1,4)、B（a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD、DC、CB。（2）求证:DC∥AB（3）当AD=BC时，求直线AB的解析式。OyX●A(1,4)●B(a,b)CD(3)DCAB ∥∴当AD=BC时有两种情况①当ADBC∥时,四边形ADCB是平行四边形,则:AE=CE,BE=DE.∴a=2∴a-1=1∴B(2,2)设直线AB的解析式为:y=kx+b(k≠0),把点A、B的坐标代入：.6262224xyABbkbkbk的解析式为：直线解得：xmyE提升能力如图,在平面直角坐标系中,函数(x>0,m是常数)的图象经过A(1,4)、B（a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD、DC、CB。（2）求证:DC∥AB（3）...