正弦函数余弦函数的性质(第课时)VIP免费

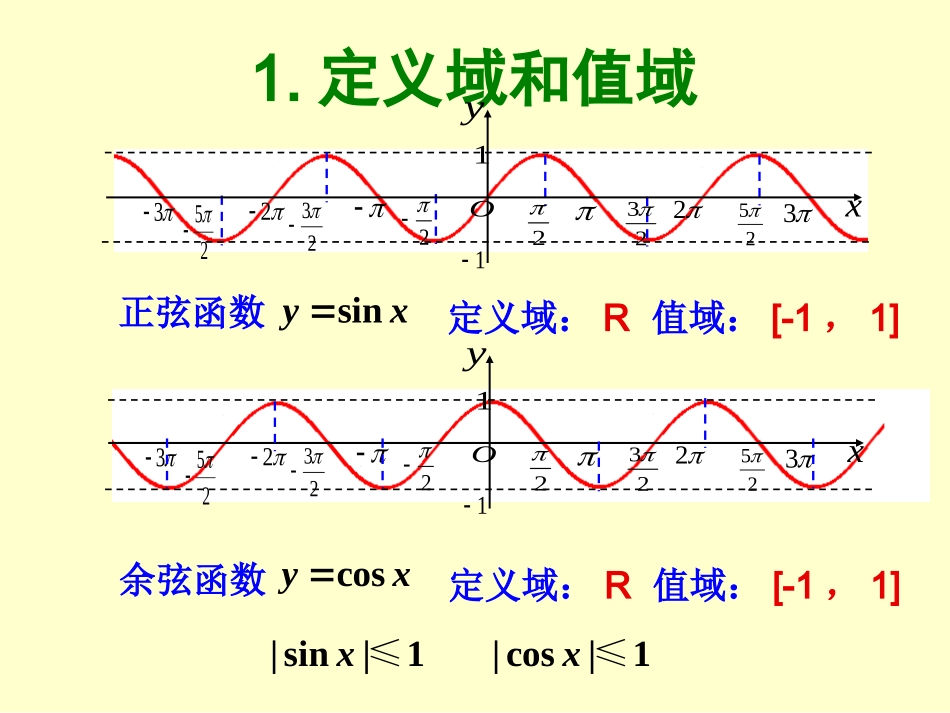
三角函数1.4.2正弦函数余弦函数的性质（一）1.定义域和值域x22322523yO23225311x22322523yO23225311正弦函数sinyx定义域：R值域：[-1，1]余弦函数cosyx定义域：R值域：[-1，1]|sin|1|cos|1≤≤xx练习P46练习2(1)2cos3x2(2)sin0.5x3cos2x1×sin0.5x[1,1]√正弦函数.余弦函数的图象和性质2o46246xy---------1-1因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，……与y=sinx,x∈[0,2π]的图象相同2,4,0,2,,2,0,4,22o46246xy---------1-1正弦函数Rxxy,sin的图象余弦函数Rxxy,cos的图象因为终边相同的角的三角函数值相同，所以y=cosx的图象在……，……与y=cosx,x∈[0,2π]的图象相同2,4,0,2,,2,0,4,2正弦、余弦函数y=sinx,y=cosx的图象正弦函数.余弦函数的图象和性质2o46246xy---------1-1因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，……与y=sinx,x∈[0,2π]的图象相同2,4,0,2,,2,0,4,22o46246xy---------1-1正弦函数Rxxy,sin的图象余弦函数Rxxy,cos的图象因为终边相同的角的三角函数值相同，所以y=cosx的图象在……，……与y=cosx,x∈[0,2π]的图象相同2,4,0,2,,2,0,4,2正弦、余弦函数y=sinx,y=cosx的图象周期函数定义：对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x+T)=f(x)那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期。2.周期性注：1、T要是非零常数2、“每一个值”只要有一个反例，则f(x)就不为周期函数（如f(x0+t)f(x0)）3、周期函数的周期T往往是多值的（如y=sinx2,4,…,-2,-4,…都是周期）4、周期T中最小的正数叫做f(x)的最小正周期（有些周期函数没有最小正周期）正弦函数是周期函数，，最小正周期是)0(2kZkk且2余弦函数是周期函数，，最小正周期是)0(2kZkk且2:期例1、求下列函数的周.,都指最小正周期若不加特别说明;,cos3)1(Rxxy;,2sin)2(Rxxy;),621sin(2)3(Rxxy)0,0.(),sin()4(ARxxAy举例3cos(2)3cosxx解：（1） ∴自变量x只要并且至少要增加到x+2π，函数3cos,yxxR的值才能重复出现.2的周期是所以，函数3cos,yxxR(2)sin(22)sin2()sin2xxxsin2,yxxR的值才能重复出现.，∴自变量x只要并且至少要增加到x+π，函数的周期是所以，函数2sin,yxxR111(3)2sin(2)2sin[()]2sin()262626xxx∴自变量x只要并且至少要增加到x+π，函数的值才能重复出现.12sin()26yx12sin(),26yxxR所以,函数的周期是π)0,0.(),cos()0,0.(),sin(ARxxAyARxxAy思考(4)2||T例求下列函数的周期：(1)y=3cosx,xR;∈1(3)2sin(),26yxxR(2)y=sin2x,xR;∈cos(2)cos,xx解:(1)cosx是以2π为周期的周期函数.3cos,yxxR的周期为23cos(2)3cos,xx这里的周期指的是最小正周期!sin(2)sin(22)xxsin(2)sin2()xxsin2yx的周期为π.(3)112sin()2sin(2)2626xx12sin()26yx的周期为４π112sin()2sin(4)2626xx另解例求下列函数的周期：1(3)2sin(),26yxxR(2)y=sin2x,x∈R;(1)y=3cosx,x∈R;解:(2)一般地，函数y=Asin(ωx+φ)(A＞0，ω＞0)的最小正周期是多少?ω2πT由上例知函数y=3cosx的周期T=2π；函数y=sin2x的周期T=π；函数y=2sin(-)的周期T=4π想一想：以上这些函数的周期与解析式中哪些量有关吗？2x6自变量的系数的绝对值πT2若则归纳总结一般地，函数及（其中为常数，且）的周期是cos()yAx,,A0,0Asin()yAx2T02T(1)()sin(2)5fxx1(2...