_正弦定理(两课时)VIP免费

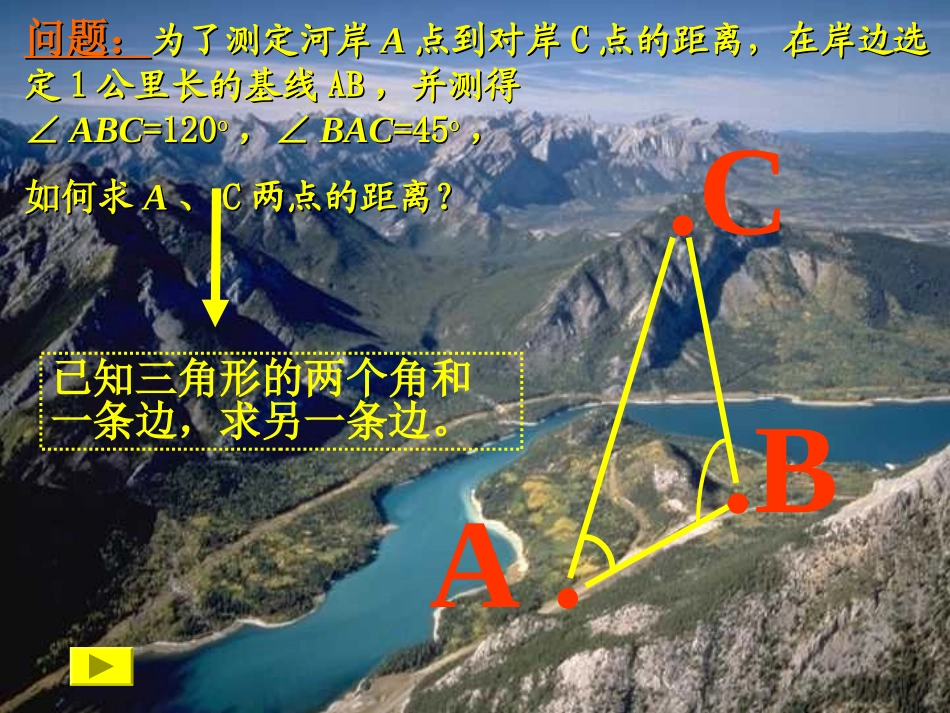
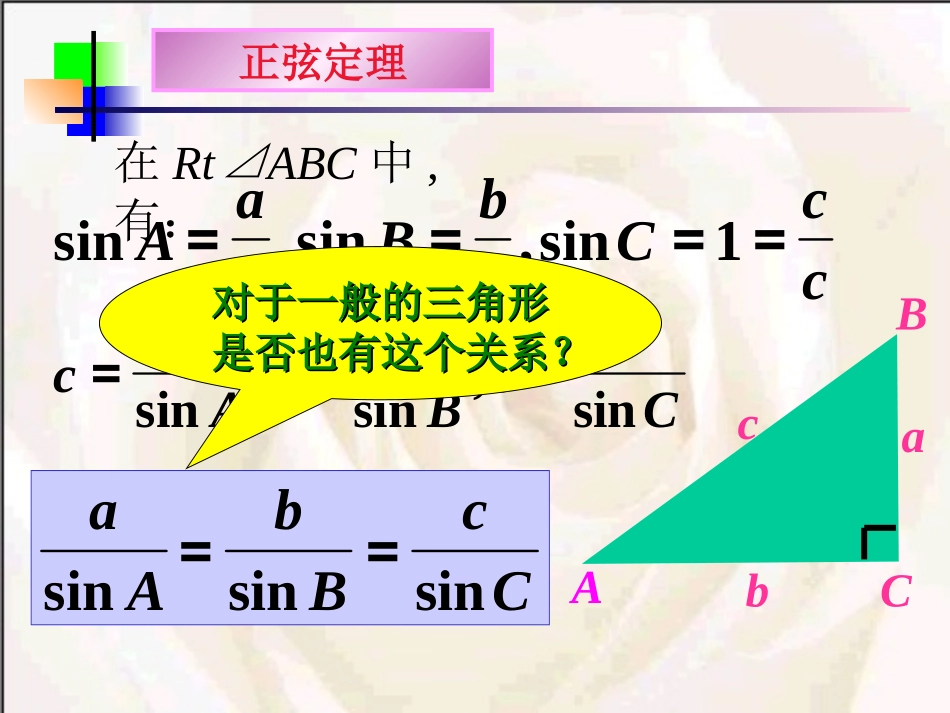
正弦定理.C.BA.问题：问题：为了测定河岸为了测定河岸AA点到对岸点到对岸CC点的距离，在岸边选点的距离，在岸边选定定11公里长的基线公里长的基线ABAB，，并测得并测得∠∠ABCABC=120=120oo，∠，∠BACBAC=45=45oo，，如何如何求求AA、、CC两点的距离？两点的距离？已知三角形的两个角和一条边，求另一条边。正弦定理正弦定理ABCabc在Rt⊿ABC中,有：ccCcbBcaA====1sin,sin,sinCccBbcAacsin,sin,sin===CcBbAasinsinsin==对于一般的三角形对于一般的三角形是否也有这个关系？是否也有这个关系？正弦定理OB/cbaCBARCcRcBCBCBAB2sin2sinsin,90'''RCcBbAaRBbRAa2sinsinsin2sin,2sin同理正弦定理＝＝asinAbsinBcsinC＝2R.=2RbsinBB`ABCbOABCbOB`ABCbO正弦定理R2CsincBsinbAsina正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即(1)已知两角和任意一边，可以求出其他两边和一角；(2)已知两边和其中一边的对角，可以求出其余边和角.CbBACbca1在△ABC中，已知c=10,A=45。,C=30。求b(保留两位有效数字）。解：∵CcBbsinsin且∴105C)(A180Bb=CBcsinsin19=30sin105sin10应用一已知两角和任一边，求其他两边和一角。A.B..Cabc5652变式训练：（1）在△ABC中，已知b=，A=，B=，求a。34560（2）在△ABC中，已知c=，A=，B=，求b。37560解：∵∴BbAasinsinaBAbsinsin=60sin45sin3=2解：∵=45)6075(180又∵CcBbsinsin∴CBcbsinsin45sin60sin32230180()CAB应用二已知两边和其中一边的对角,求其余边和角解：BbAasinsin231630sin316sinsinaAbBＢ＝60°,或Ｂ＝120°当时Ｂ＝60°C=90°，.32cC=30°.16sinsinACac2、已知a=16，b=，A=30°，解三角形。316当Ｂ＝120°时B16300ABC16316∵∴∴注意讨论多解注意讨论多解在上题中，将已知条件改为以下几种情况，结果如何？（1）b＝20，A＝60°，a＝20√3;（2）b＝20，A＝60°，a＝10√3;（3）b＝20，A＝60°，a＝15.60°ABCb（1）b＝20，A＝60°，a＝20√3sinB＝＝，bsinAa12B＝30°或150°，∵150°＋60°>180°，∴B＝150°（舍）60°2020√3ABC（2）b＝20，A＝60°，a＝10√3sinB＝＝1，bsinAaB＝90°.B60°AC20（3）b＝20，A＝60°，a＝15.sinB＝＝，bsinAa2√332√33∵>1，∴无解.60°20AC已知边a,b和角Ａ，求其他边和角．Ａ为锐角ab一解a≤b无解ＡＢＣbaＡＣbaＡＣabＡＢＣabＡＢ１Ｂ２ＣabＡＢＣab正弦定理（3）已知c＝2，A＝45°，a＝，则B＝_____________.（2）已知c＝2，A＝120°，a＝2√3，则B＝____.（1）已知c＝√3，A＝45°，B＝75°，则a＝____.√230°1.在△ABC中，2√6375°或15°2.(1)3,1,60,,;ABCbcBaAC在中，已知求和，9030,,60,ACCBCBcb，为锐角，,sinsinbcBC解：sin1sin601sin23cBCb222bca思考思考.,45,22,32)2(ABba求已知(3)20,28,120,.abA已知解这个三角形sinsinaBAb解：232245sin32)(,大边对大角CAba12060或AsinsinbABa解：20120sin287310本题无解思考思考13练习2、在ABC中，若a=2bsinA，则B＝()A、B、C、D、36653326或或练习1、在ABC中，若A：B：C=1：2：3，则a:b:c＝()A、1:2:3B、3:2:1C、1::2D、2::133A、等腰三角形B、直角三角形C、等腰直角三角形D、不能确定2223.,sinsinsin,()ABCABCABC练习在中若则的形状是CCB二个——已知两角和任一边——已知两边和其中一边的对角一个——正弦定理CcBbAasinsinsin定理应用课时小结课时小结（只有一解）（有一解，两解，无解）小结2.正弦定理可解以下两种类型的三角形：（1）已知两角及一边；（2）已知两边及其中一边的对角.1.（其中R为⊿ABC外接圆的半径）正弦定理是解斜三角形的工具之一.＝＝asinAbsinBcsinC＝2R