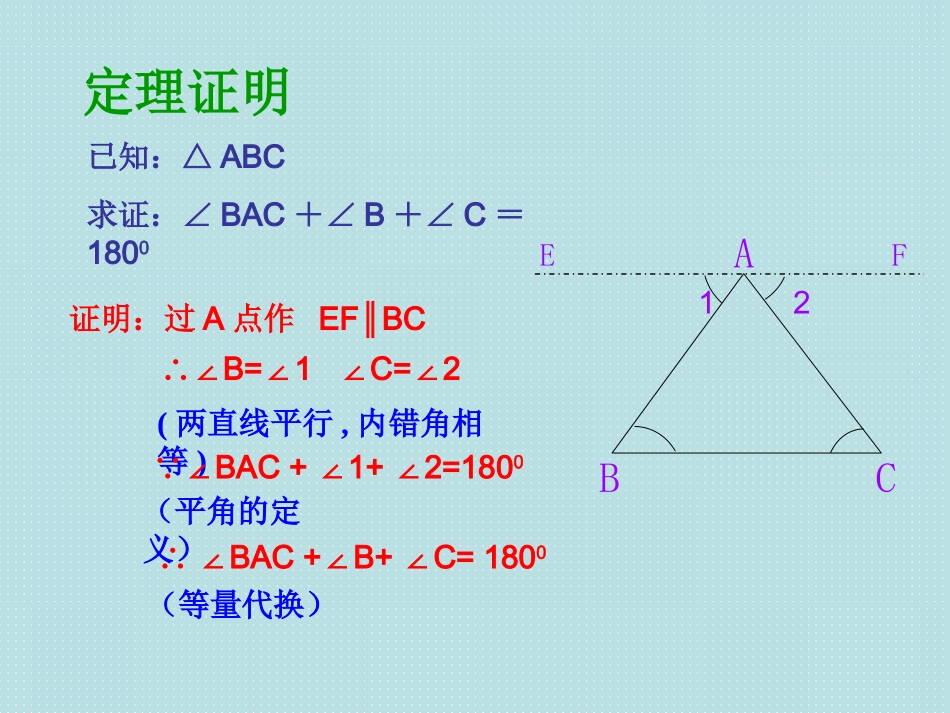
教学片断知识回顾:1:两直线平行,同位角相等2:两直线平行,内错角相等3:两直线平行,同旁内角互补定理证明已知:△ABC求证:∠BAC+∠B+∠C=1800证明:过A点作EFBC∥EFABC12∴∠B=1C=2∠∠∠∴∠BAC+B+C=180∠∠0(两直线平行,内错角相等)∵∠BAC+1+2=180∠∠0(等量代换)(平角的定义)二、三角形的内角和定理:三角形三个内角的和等于1800。ABC∠A+∠B+∠C=18002、已知:如图,在△ABC中,∠A=100°,∠B=C∠。求:则∠B、∠C的度数为。ABC三:例题讲解:1、在三角形ABC中,∠A=50°,∠B=60°,则∠C的度数为。五、随堂跟踪练习1、在△ABC中,若∠A=300B=∠400则∠C=。2、如图:∠1=。11002803204401480已知:△ABC求证:∠A+∠B+∠ACB=1800∴∠2=∠B(两直线平行,同位角相等)又∵∠1+∠2+∠ACB=1800(平角的定义)∴∠A+∠B+∠ACB=1800(等量代换)ABCDE12课后思考,请用另外的方法证明证明:延长BC到D,过C点作CEBA∥∴∠1=∠A(两直线平行,内错角相等)