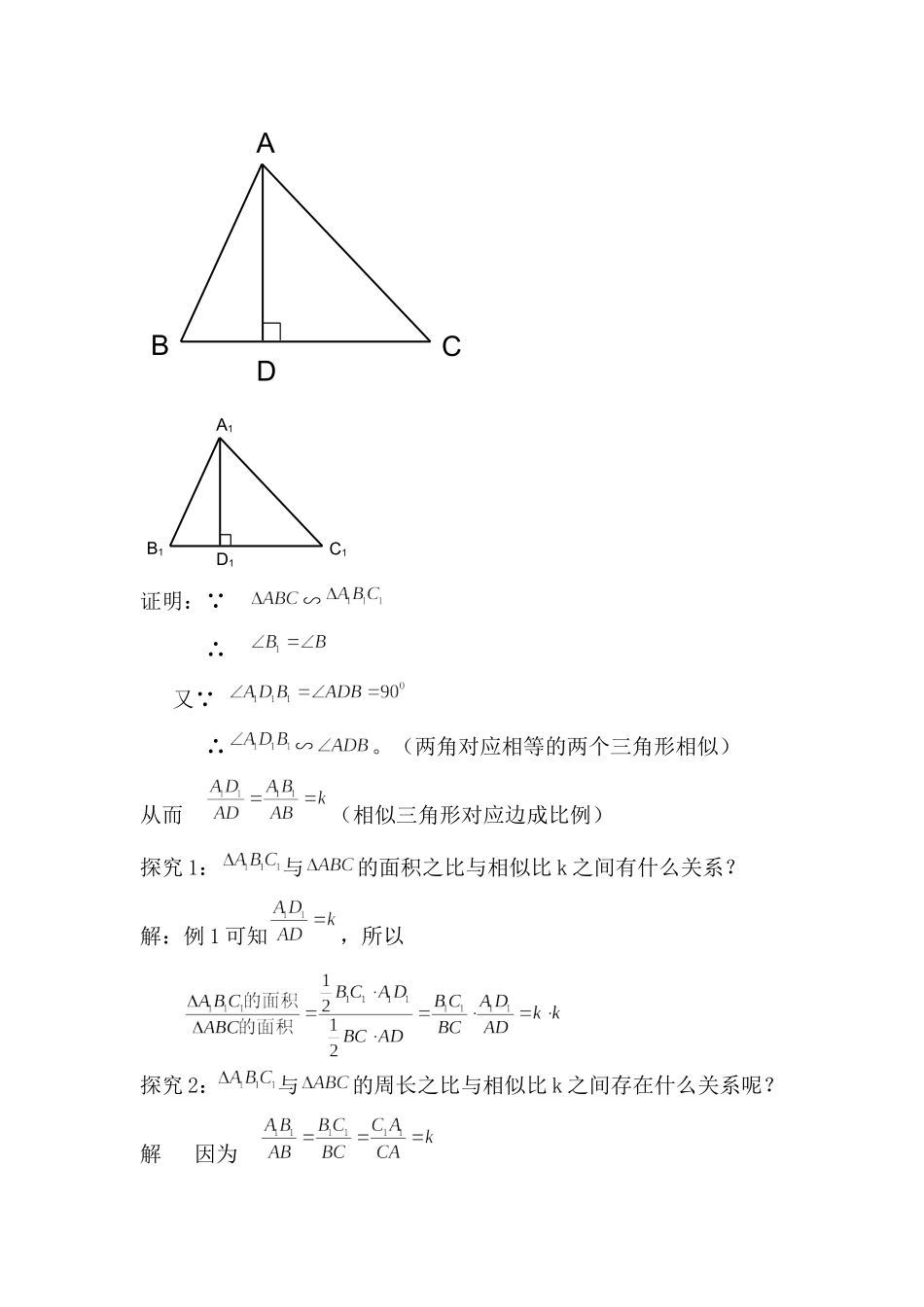
相似三角形判定定理2一、教学目标知识与能力:(1)掌握三角形相似的判定定理2。(2)会用相似三角形判定定理2来判断及计算。过程与方法:经历相似三角形判定定理2的探索过程,培养学生的观察、分析、比较、归纳能力,渗透类比、转化及数形结合的数学思想方法,体验事物间特殊与一般的关系。情感态度与价值观:通过实物演示和多媒体教学手段,提高学生学习数学的兴趣和积极性,培养学生科学严谨的治学态度。二、教学重点、难点重点:相似三角形判定定理2的探索及其应用。难点:相似三角形判定定理2的应用。三、教学过程(一)创设情境(趣味问题引入,配以动画演示)古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.(二)探究新知1.观察猜想引导学生思考:判定三角形全等的方法有哪些呢?判定两个三角形相似有哪些方法呢?是否存在判定两个三角形相似更简便的方法呢?假如当条件只有角这个元素时,能不能判定两个三角形相似呢?观察1:学生观察自己的一对直角三角板。问题1:你们的两块三角板是否相似呢?观察2:学生观察自己与老师的锐角为的直角三角板。问题2:这两块三角板是否相似呢?O′B′BA′AO问题3:这两个三角形相似是因为哪些元素的关系而相似?问题4:任意两个三角形三个角相等,它们一定相似吗?2.分组讨论(每两人一组)画一画:同桌每人用量角器在纸上任意画一个三角形,要求同桌所画三角形的三对角分别对应相等,用刻度尺量出三边长度,并与同桌比较,看看两个三角形的对应边是否成比例,你能得出什么结论呢?3.归纳定理:(学生总结,教师纠正)三角形相似的判定定理2:如果一个三角形与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等的两个三角形相似。4.解决问题这时再请学生回头看引入中的问题,利用判定定理2让学生自己独立完成。(三)应用巩固例1.已知:在和中,,,,。求证:∽。例2:如图,在△ABC中,EF∥BC,求证:△AEF∽△ABC例3.如图,∽,相似比为k,分别作BC,上的高AD,。求证:ADCEB证明:∵∽∴又∵∴∽。(两角对应相等的两个三角形相似)从而(相似三角形对应边成比例)探究1:与的面积之比与相似比k之间有什么关系?解:例1可知,所以探究2:与的周长之比与相似比k之间存在什么关系呢?解因为ACBDA1C1B1D1所以,从而。(四)分层练习基础练习:1.填空:(1)在△ABC与△DEF中,,,,。△_____∽△DEF。(2)已知△ABC∽△DEF,且面积之求证比为4:25,则△ABC与△DEF的相似比为________.2.已知△ABC∽△DEF,它们的周长分别为60cm和72cm,且AB=15cm,EF=24cm,求BC,AC,DE,DF的长。3.若∽,且=3,=4.5,且,求的面积。提高练习:如图:在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且AFE=B.(1)求证:△ADF∽△DEC.(2)若AB=4,AD=,AE=3,求AF的长.(挑战中考)如图:△ABC和△DEF均为正三角形,D、E分别在AB、BC上,请找出一个与△DBE相似的三角形并证明。(五)小结归纳1.通过本节课的学习,你学会了哪些知识?ADCBFEACFBDEHG2.通过本节课的学习,你最大的体验是什么?3通过本节课的学习,你掌握了哪些学习数学的方法?(六)布置作业1.P81的习题3.3A组第3题,B组第3题2.(任选一题)(1)写一篇数学日记,记下你今天的感想.(2)利用”相似三角形”试画一幅画,作为教室的装饰画。(3)利用图书、网络资源查找并记录一些相似三角形在实际生活中应用的事例。