高中数学必修4平面向量课件--向量的数乘VIP免费

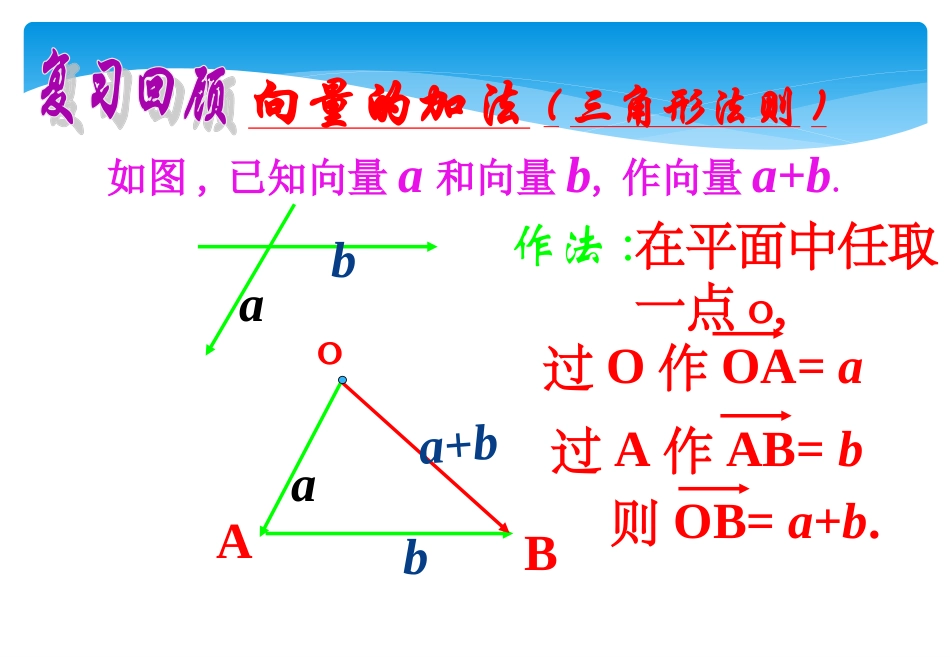
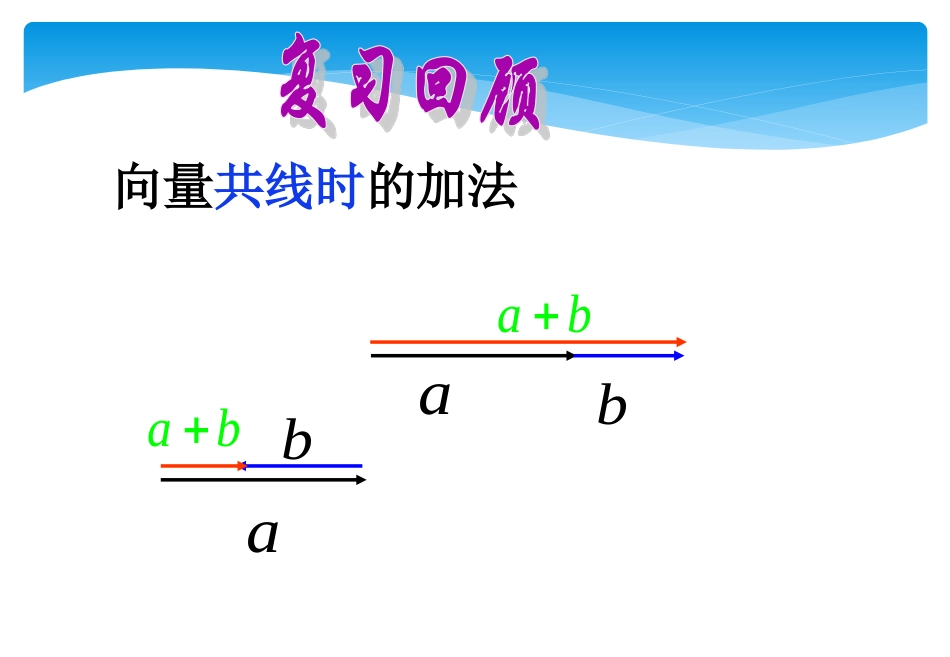
24/12/14向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.ab作法:在平面中任取一点o,aAbBa+b过O作OA=a则OB=a+b.过A作AB=bo向量共线时的加法abbaabba向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.a作法:在平面中任取一点o,oaAbBb以OA,OB为边作平行四边形a+bC过O作OA=a过O作OB=b则对角线OC=a+b向量的减法(三角形法则）如图,已知向量a和向量b,作向量a-b.ab作法:在平面中任取一点o,oaAbBa-b过O作OA=a过O作OB=b则BA=a-b位移、力、速度、加速度等都是向量，而时间、质量等都是数量，这些向量与数量的关系，常常在物理公式中出现，如力与加速度的关系F=ma，位移与速度的关系s=vt，这些公式都是实数与向量间的关系、实数与实数可以进行加法、减法、求积等运算，实数与向量能否进行加法、减法、求积运算呢？若能进行运算，运算的规则又如何呢？引入新课§2.1.4§2.1.4向量数乘向量数乘§2.1.4§2.1.4向量数乘向量数乘高中数学高中数学44=a3ABCDa++aaaa(-)(-)(-)a3-ABCDaaa++＝相同向量相加后,和的长度与方向有什么变化?aaaaaaOOAABBCC3aa-3a-a-a-a-a-a-aPPQQMMNNaa一般地，实数一般地，实数λλ与向量与向量aa的的乘乘积积是一个是一个向量向量，，这种运算叫做这种运算叫做向量的数乘运算向量的数乘运算，记作，记作λλaa，，它的它的长度长度和和方向方向规定如下：规定如下：(1)|(1)|λλaa|=||=|λλ||||aa||(2)(2)当当λ>0λ>0时时,,λλaa的方向与的方向与aa方向相同；方向相同；当当λ<0λ<0时时,,λλaa的方向与的方向与aa方向相反；方向相反；特别地特别地，当，当λ=λ=00或或aa=0=0时时,,λλaa=0=0a≠0λλaa中实数的中实数的λλ,,叫做向量叫做向量aa的的系数系数？数乘向量的几何意义就是把向量沿的方向或反方向放大或缩短.若,当沿的方向放大了倍.当沿的方向缩短了倍.当,沿的反方向放大了倍.当沿的反方向缩短了倍.由其几何意义可以看出用数乘向量能解决几何中的相似问题.0a时，1时，〈〈10时1a时，〈〈01aaaaaλa复习回顾:实数乘法的运算律1、交换律：ab=ba2、结合律：a(bc)=(ab)c=b(ac）3、分配律：a(b+c）=ab+acaa2a6)2(3a一般地:)2(3aa6=aa)()(abba)(2baa2b2baba22)(2baba)(一般地:aa5a2a3一般地：aaa)(aaa32)32(22aa11(b)=b设设a,ba,b为任意向量，为任意向量，λ,μλ,μ为任意为任意实数实数，则有：，则有：①①λλ((μμaa)=()=(λμλμ))aa((结合律结合律))②②((λλ++μμ))aa==λλaa++μμaa((第一分配律第一分配律))③③λλ((aa++bb)=)=λλaa++λλbb((第二分配律第二分配律))对于任意的向量以及任意实数恒有ab,、12、、，向量的加、减、数乘运算统称为向量的线性运算。基础知识反馈aaC.的方向相反与aaA.的方向相同与aa2B.(2).设是非零向量,是非零实数,下列结论正确的是().aaD.a(1).下列四个说法正确的个数有().B.2个A.1个C.3个D.4个;bmambambam）（，恒有、和向量对于实数;),(baRmbmam则有若;,0),(nmaRnmanam则有、若;)(anamanmanm，恒有和向量、对于实数BC例1计算下列各式a21)2();(3)(2babaaaaa)1()212(21)2((1)(2)(3)例题分析计算下列各式a4)3)(1(ababa)(2)(3)2(a12b5)23()32)(3(cbacbacba25反馈演练))(())()(4(2121bcttbcttctbt2122例2设未知向量,解方程5(+)+3(-)=0解:原式可变形为bax358xxabx5+5+3-3=0bax8385bxax反馈演练:教材95页练习A第3题答案:(1)(2)(3)a32ba43cba7171214例题分析例３:若3m+2n=a,m-n=b,其中,b是已知向量,求m,n分析:此题可把已知条件看作向量的方程,通过解方程组获得aanm23bnm3bam112113解：记①，②bnm3933②得③,113111ban①-③得...