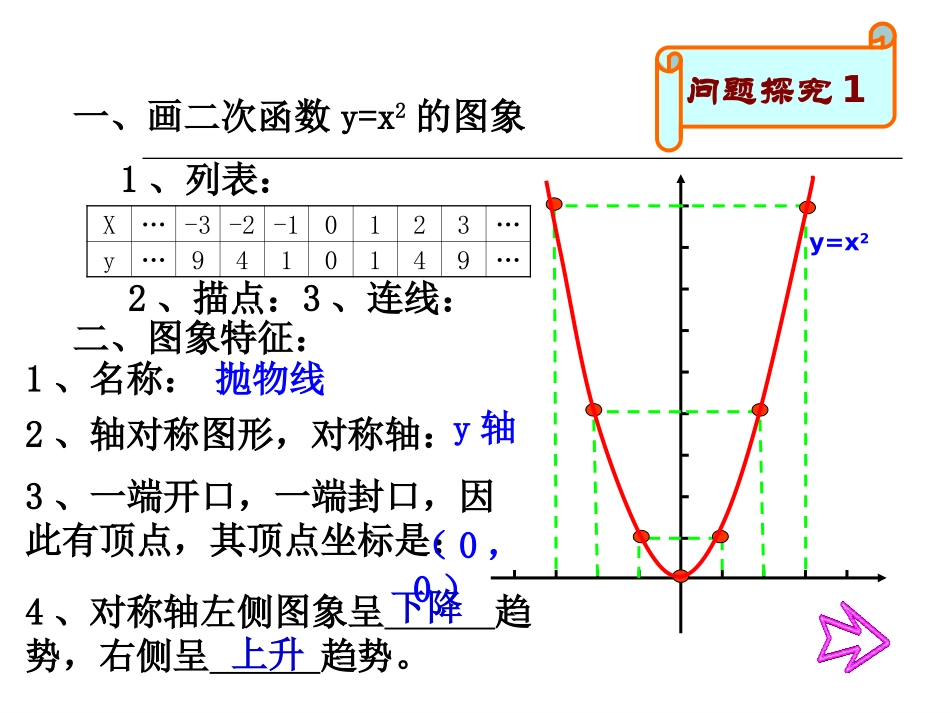
研究函数性质的一般策略:数形结合忠县新生初级中学陈联善提出问题26.1二次函数y=ax2的图象与性质问题探究1一、画二次函数y=x2的图象X…-3-2-10123…y…9410149…1、列表:2、描点:3、连线:二、图象特征:1、名称:抛物线2、轴对称图形,对称轴:y轴3、一端开口,一端封口,因此有顶点,其顶点坐标是:(0,0)y=x24、对称轴左侧图象呈趋势,右侧呈趋势。下降上升问题探究1在同一直角坐标系中,画出函数y=x2与y=-x2的图象,观察并比较两个图象,你发现有什么共同点?又有什么区别?y=x2y=-x2相同点:不同点:对称轴相同,顶点相同开口方向不同a>0时,开口向上;a<0时,开口向下。联系:它们关于x轴对称问题探究2在同一直角坐标系中,画出函数y=2x2与y=-2x2的图象,观察并比较两个图象,你发现有什么共同点?又有什么区别?y=2x2y=-2x2Oyxy=x2y=-x2y=x2y=-x2相同点:对称轴都是y轴;顶点都是(0,0)不同点:开口方向不一样:a>0,开口向上;a<0,开口向下。∣a∣越大,开口越小;∣a∣越小,开口越大。∣a∣相同,则开口大小也一样。开口大小不一样:夯实基础填空:1、抛物线开口向,对称轴是,当x<0时,y随x增大而,当x>0时,y随x增大而,当x=时,y有最值是。y=x22、抛物线关于x轴对称的抛物线是,其开口向,对称轴是,当x<0时,y随x增大而,当x>0时,y随x增大而,当x=,y有最值是。y=x23、若抛物线y=ax2过点(-2,8),则抛物线的解析式为,当x=3时,y=;当y=4时,x=。上y轴减小增大0小0下y轴增大减小00大y=-x2y=2x218或-开口大小由决定归纳小结二次函数y=ax2的图象与性质︱a︱开口方向由决定二次函数y=ax2图象是一条,其对称轴是,顶点是。原点抛物线y轴时,开口向上时,开口向下a的符号a>0a<0函数有最点函数有最点对称轴左侧呈趋势对称轴右侧呈趋势对称轴左侧呈趋势对称轴右侧呈趋势越大,开口越;越小,开口越;相同,则开口大小也。小最低最高上升下降下降上升︱a︱︱a︱︱a︱大相同能力拓展xyo抛物线y=mx2过点(1,2),则其解析式为;抛物线y=kx2过点(2,1),则其解析式为;xyoy=2x2y=x2现由四条直线x=1,x=2,y=1,y=2围成了一个正方形,若抛物线y=ax2与正方形必有交点,则a的取值范围是。ABCDy=2x2y=x2一、填空题:能力拓展二、解答题:现有一抛物线形拱桥,平时河水离拱顶16米,水面宽8米,当洪水到来时,水面宽6米,此时监测到水面每小时上涨2米,问几小时后,洪水将完全封住桥洞?xyOMP8米6米16米解:以拱顶所在水平线为x轴,铅垂线为y轴建立直角坐标系。设平时水位与桥拱所在抛物线的右侧交点为P,则P点坐标为(4,-16);设抛物线的表达式为y=ax2.则根据P点得其解析式为y=-x2.设洪水水位与抛物线右侧交点为M,则M的横坐标为3,将其代入y=-x2中得y=-9∴洪水完全封住桥洞时间为:9÷2=4.5(小时)答:洪水完全封住桥洞要4.5小时。作业布置必做题:1.如何画出函数y=ax2的图象?2.函数y=ax2具有哪些性质?3.谈谈你对本节课学习的体会。选做题:有一抛物线形的隧洞,其解析式为y=ax2,洞拱跨度为12米,洞高4米,按规定,通过该洞的货车最高处与洞拱之间的距离不得小于0.5米,今有一宽为3米,高为3米的货车能否通过此隧洞?为什么?End