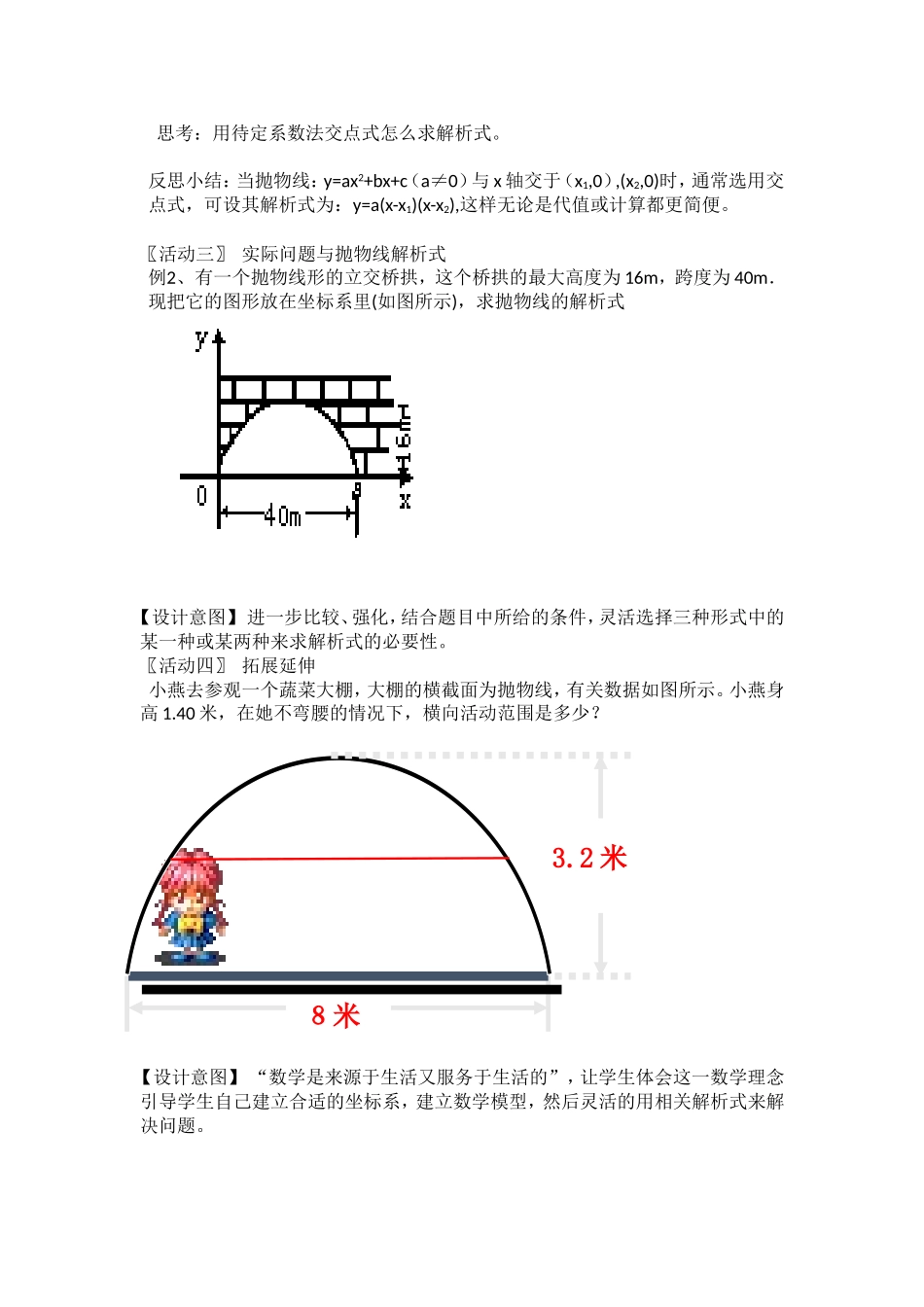
用待定系数法求二次函数的解析式麻城市闵集中学董亚玲【教学目标】1能根据题目中所给条件,用交点式求二次函数解析式;2.掌握二次函数解析式的三种表达式,并能灵活选用解题。【教学重难点】〖教学重点〗用待定系数法和交点式求二次函数解析式。〖教学难点〗灵活选用恰当的形式求二次函数的解析式。【学情分析】本课是继学习了用一般式、顶点式求二次函数解析式后,学习的另一种表现形式——交点式。学生已有了用待定系数法求解析式的经验,所以用待定系数法求解析式的方法不是问题,而难点是现在三种解析式放在一起该如何选择,从而灵活巧妙简捷地解题。【教学设计】一、复习旧知,引入新课(1)用待定系数法求解析式的一般步骤:a、设b、代c、解d还原(2)二次函数解析式的表现形式:一般式:y=ax2+bx+c(a≠0)(通常给定抛物线上任意三点时选用.)顶点式:y=a(x-h)2+k(a≠0)(通常给定抛物线的顶点或对称轴或最值时选用)二、合作探究,讲授新知〖活动一〗求出表格中各条抛物线与x轴的交点,并谈谈你的发现?交点式(x1,0)(x2,0)【设计意图】依解析式得交点,反之依交点得解析式,发现并运用规律。〖活动二〗例1、抛物线交x轴于A(-1,0)、B(1,0),并经过点M(0,1),求它的解析式。yMABx抛物线的解析式抛物线与x轴的交点Y=a(x-1)(x-3)(a≠0)Y=a(x-2)(x+1)(a≠0)Y=a(x+4)(x+6)(a≠0)思考:用待定系数法交点式怎么求解析式。反思小结:当抛物线:y=ax2+bx+c(a≠0)与x轴交于(x1,0),(x2,0)时,通常选用交点式,可设其解析式为:y=a(x-x1)(x-x2),这样无论是代值或计算都更简便。〖活动三〗实际问题与抛物线解析式例2、有一个抛物线形的立交桥拱,这个桥拱的最大高度为16m,跨度为40m.现把它的图形放在坐标系里(如图所示),求抛物线的解析式【设计意图】进一步比较、强化,结合题目中所给的条件,灵活选择三种形式中的某一种或某两种来求解析式的必要性。〖活动四〗拓展延伸小燕去参观一个蔬菜大棚,大棚的横截面为抛物线,有关数据如图所示。小燕身高1.40米,在她不弯腰的情况下,横向活动范围是多少?【设计意图】“数学是来源于生活又服务于生活的”,让学生体会这一数学理念引导学生自己建立合适的坐标系,建立数学模型,然后灵活的用相关解析式来解决问题。3.2米8米BCOOABAOMOBABA三、总结梳理,内化新知学习二次函数一般的方法与规律:A、二次函数解析式的三种形式:(1)一般式:y=ax2+bx+c(a≠0)(2)交点式:y=a(x-x1)(x-x2)(a≠0)(3)顶点式:y=a(x-h)2+k(a≠0)在求二次函数解析式时,根据题目中的条件,灵活设出解析式,以便简捷地求出其解析式。B、用待定系数法求解析式的步骤:(1)设(2)代(3)解(4)还原四、达标检测,巩固新知1、二次函数y=ax2+bx+c(a≠0)的部分对应值如下表:x…-3-20135…y……(1)请完善表格中的数据;(2)求其解析式。有几种方法可以选择,其中哪种更简捷?8米3.2米8米3.2米8米3.2米8米3.2米y=﹘2、函数抛物线的对称轴为直线x=3,且图像经过A(1,0)、B(0,3)。(1)求其解析式;(2)设其顶点为c,求S△ABC。