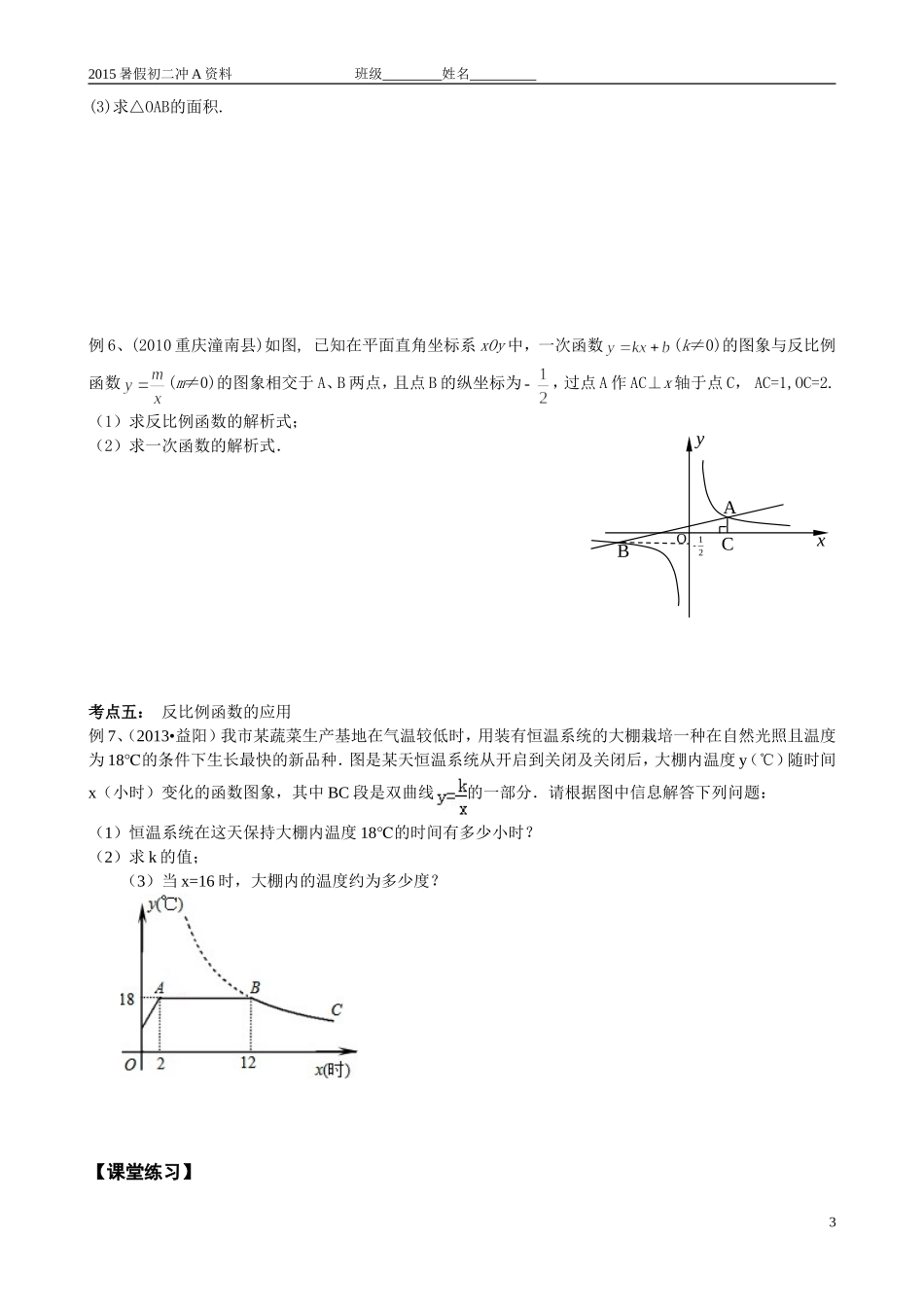
2015暑假初二冲A资料班级姓名第九讲反比例函数【知识梳理】1.反比例函数的定义、图象和性质:(1)定义:形如的函数叫做反比例函数。例如。(2)图象:双曲线。(3)性质:①>0时,图象位于___________,在每一个象限内,随增大而_______00②<0时,图象位于________;在每一个象限内,随增大而_________,③两支曲线无限接近于坐标轴但永远不能到达坐标轴。2.反比例函数=(k≠0)中的意义:反比例函数=(k≠0)中系数的几何意义,即过双曲线=(k≠0)上任意一点引轴、轴的垂线,所得矩形面积为││。3.用待定系数法求反比例函数解析式;4.分析实际问题中的反比例函数关系,建立反比例函数模型,利用反比例函数的性质解决实际问题。【经典考题】考点一:反比例函数的定义例1、(1)下列函数中,是反比例函数的是()A、B、C、D、(2)(2009柳州)反比例函数xmy1的图象经过点(2,1),则m的值是.(3)(2013青岛)已知矩形的面积为36cm2,相邻的两条边长为xcm和ycm,则y与x之间的函数图像大致是()考点二:反比例函数的图像与性质例2、(1)(2008常州)若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是()A.-1B.3C.0D.-3(2)(2007南昌)对于反比例函数,下列说法不正确的是()A.点在它的图象上B.它的图象在第一、三象限C.当时,随的增大而增大D.当时,随的增大而减小(3)(2010长沙)已知反比例函数1myx的图象如图,则m的取值范围是.1oyxyxoyxB1123312O第13题图yAOBCPx2015暑假初二冲A资料班级姓名(4)(2010台州)反比例函数图象上有三个点,,,其中,则,,的大小关系是()A.B.C.D.考点三:反比例函数的比例系数k的几何意义例3、(1)(2013,娄底)如图,已知A点是反比例函数(0)kykx的图象上一点,ABy轴于B,且ABO△的面积为3,则k的值为_____________.(2)(2008宁波)如图,正方形的边长为2,反比例函数过点,则的值是()A.B.C.D.(3)(2013,永州)如图,两个反比例函数4yx和2yx在第一象限内的图象分别是1C和2C,设点P在1C上,PAx轴于点A,交2C于点B,则△POB的面积为(4)(2013•淄博)如图,矩形AOBC的面积为4,反比例函数kyx的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是()(A)4yx(B)2yx(C)1yx(D)12yx考点四:反比例函数与一次函数综合例4、(1)(2010青岛市)函数与(a≠0)在同一直角坐标系中的图象可能是().A.B.C.D.(2)(2011浙江杭州)如图,函数和函数的图象相交于点M(2,m),N(-1,n),若,则x的取值范围是()A.B.C.D.例5、(2013四川)如图,已知A(-4,2)、B(n,-4)是一次函数的图象与反比例函数的图象的两个交点.(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.2ABP1CO2C14第题图xyCOABxOyxyOyxOyxO2015暑假初二冲A资料班级姓名(3)求△OAB的面积.例6、(2010重庆潼南县)如图,已知在平面直角坐标系xOy中,一次函数(k≠0)的图象与反比例函数(m≠0)的图象相交于A、B两点,且点B的纵坐标为,过点A作AC⊥x轴于点C,AC=1,OC=2.(1)求反比例函数的解析式;(2)求一次函数的解析式.考点五:反比例函数的应用例7、(2013•益阳)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)求k的值;(3)当x=16时,大棚内的温度约为多少度?【课堂练习】3xyABCO21-题图232015暑假初二冲A资料班级姓名1.(2006株洲)若双曲线过点P(3,2),则k的取值是.2.(2007株洲)已知一次函数与双曲线相交于A、B两点,若已知一个交点A为(2,1),则另一个交点B的坐标为.3.(2008株洲)已知函数的图象如下,当时,的取值范围是()A.B.C.或D.或4.(2009株洲)反比例函数图象如图所示,则这个反比例函数的解析式是.5.(2013株洲)已知点A(1,...