(公开课)131函数的单调性和最大小值(1)VIP免费

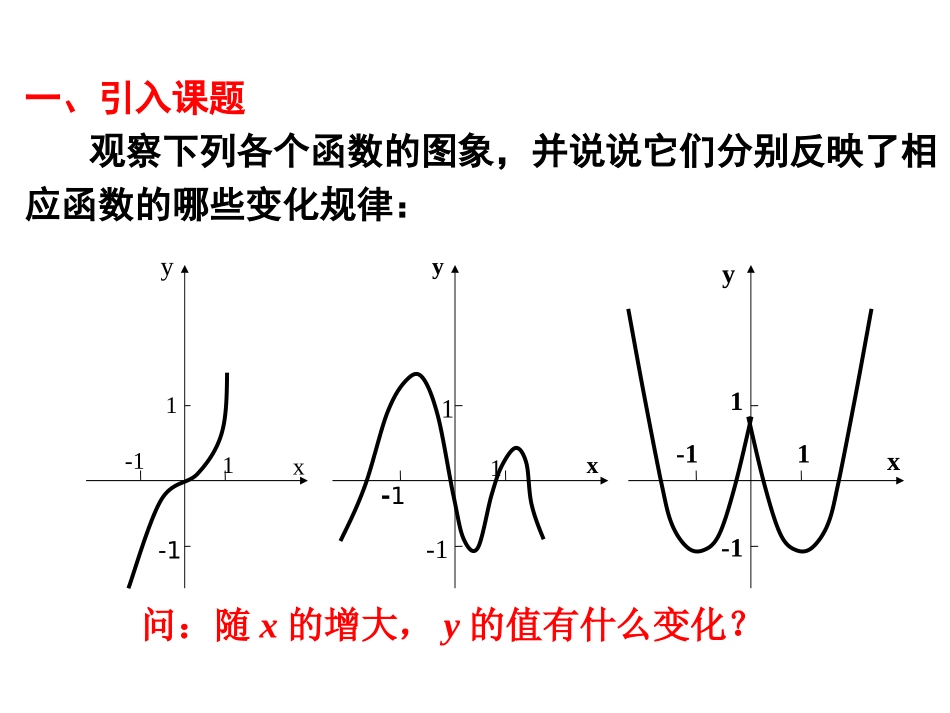
------函数的单调性一、引入课题观察下列各个函数的图象，并说说它们分别反映了相应函数的哪些变化规律：yx11-1yx1-11-1问：随x的增大，y的值有什么变化？x1-11y-1-1画出下列函数的图象，观察其变化规律：1．f(x)=x①从左至右图象上升还是下降______?②在区间____________上，随着x的增大，f(x)的值随着________．2．f(x)=-2x+1①从左至右图象上升还是下降______?②在区间____________上，随着x的增大，f(x)的值随着________．上升（-∞，+∞）增大下降（-∞，+∞）减小3．f(x)=x2①在区间____________上，f(x)的值随着x的增大而________．②在区间____________上，f(x)的值随着x的增大而________．x…-4-3-2-101234…f(x)…16941014916…(-∞,0]减小（0，+∞）增大y246810O-2x84121620246210141822D对区间D内x1，x2，当x1单调区间注意：①函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质；②必须是对于区间D内的任意两个自变量x1，x2；③函数的单调性是相对某个区间而言，不能直接说某函数是增函数或减函数。下列说法是否正确？请画图说明理由。（1）如果对于区间（0，+∞）上的任意x有f(x)>f(0),则函数在区间（0，+∞）上单调递增。（2）对于区间（a,b）上的某3个自变量的值x1,x2,x3,当时，有则函数f(x)在区间（a,b）上单调递增。123()()()()()fafxfxfxfb123axxxb2．单调性与单调区间如果函数y=f(x)在某个区间D上是增函数或减函数，那么就说函数y=f(x)在这一区间具有（严格的）单调性，区间D叫做y=f(x)的单调区间：注意：⑴函数的单调区间是其定义域的子集；⑵应是该区间内任意的两个实数，忽略需要任意取值这个条件，就不能保证函数是增函数（或减函数），例如，图5中，在那样的特定位置上，虽然使得,但显然此图象表示的函数不是一个单调函数；1x2x)(1xf)(2xf)(xf图5yx12()()fxfx⑶几何特征：在自变量取值区间上，若单调函数的图象上升，则为增函数，图象下降则为减函数.思考1：一次函数的单调性，单调区间：)0(kbkxy思考2：二次函数的单调性，单调区间：)0(2acbxaxy（二）典型例题例1如图6是定义在闭区间[-5，5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一单调区间上，函数y=f(x)是增函数还是减函数.)(xf6图yx-5-2135O•书写单调区间时，注意区间端点的写法。对于某一个点而言，由于它的函数值是一个确定的常数，无单调性可言，因此在写单调区间时，可以包括端点，也可以不包括端点。但对于某些不在定义域内的区间端点，书写时就必须去掉端点。练习：判断函数的单调区间。2()2fxxxxxxxf2)(2y21o单调递增区间：单调递减区间：]1,(),1[）上是增函数。，（在区间证明函数xxf12)(.例2内任意是区间设),(,x21x121212()()(21)(21)2(x)fxfxxxx0x,2121xxx0)()(21xfxf)()(21xfxf即证明：。两个实数，且x21x),(12)(在区间则函数xxf是增函数。（取值）（作差）（下结论...