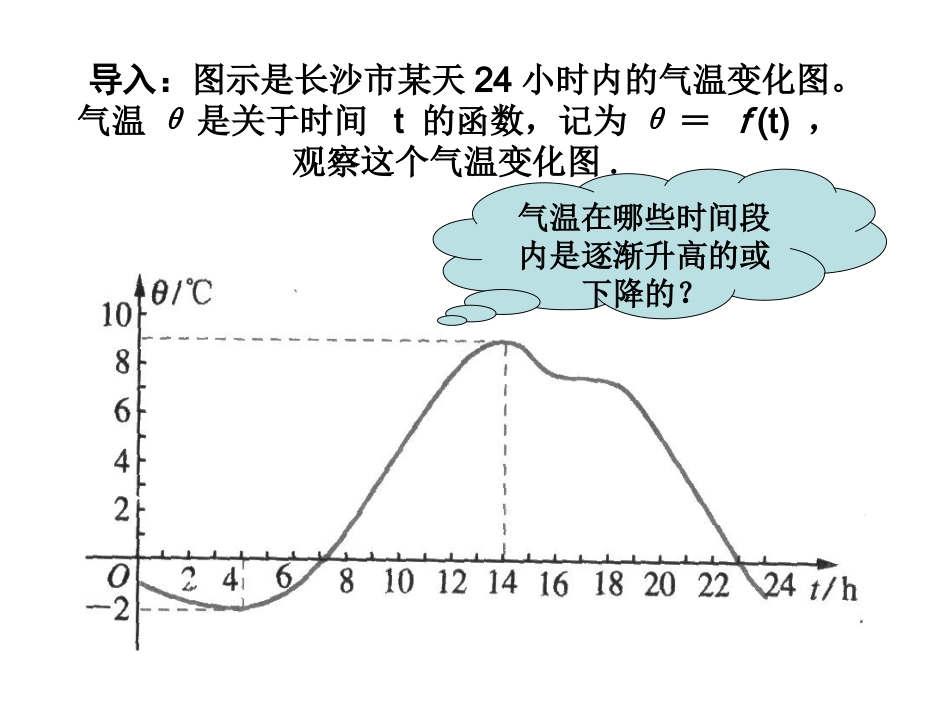
课题:函数的单调性课题:函数的单调性人教A版高一数学必修一导入:图示是长沙市某天24小时内的气温变化图。气温θ是关于时间t的函数,记为θ=f(t),观察这个气温变化图.气温在哪些时间段内是逐渐升高的或下降的?一.学生练习:画出下列函数图象1.一次函数f(x)=x的图象特点:函数图象由左至右是上升的2.二次函数f(x)=x²的图象特点:函数图象在y轴左侧是下降的,在y轴右侧是上升的讨论根据上述函数图象的特点,如何来描述图象的“上升”与下降“呢?以二次函数为例,由其图象我们可以发现:图象在y轴左侧“下降”,也就是,在区间(-∞,0]上,随着x的增大,相应的f(x)反而随着减小;图象在y轴右侧“上升”,也就是,在区间(0,+∞)上,随着x的增大,相应的f(x)也随着增大.提出问题:如何利用函数的解析式f(x)=x²描述“随着x的增大,相应的f(x)随着减小”“随着x的增大,相应的f(x)也随着增大”结合对图象的理解,我们可以这样描述“在区间(0,∞)上,随着x的增大,相应的f(x)也随着增大“:在区间(0,+∞)上,任取两个x₁,x₂,得到f(x)₁=x₁²,f(x)=x₂₂²,当x₁<x₂有f(x)₁<f(x)₂,这时,我们就说函数f(x)=x²在区间(0,+∞)上是增函数.问:能否仿照上面的描述说明函数f(x)=x²在区间(-∞,0]上是减函数呢?在区间(-∞,0]上,任取两个x₁,x₂,得到f(x)₁=x²,₁f(x)=₂x²₂当x₁<x₂时,有f(x)₁>f(x)₂,我们就说函数f(x)=x²在区间(-∞,0]上是减函数.新知识:1、增函数与减函数定义:对于函数y=f(x)的定义域I内某个区间D上的任意两个自变量的值x₁,x₂⑴若当x₁<x₂时,都有f(x)₁<f(x)₂,那么就说函数f(x)在区间D上是增函数⑵若当x₁<x₂时,都有f(x)₁>f(x)₂,那么就说函数f(x)在区间D上是减函数.Oxyf(x₁)f(x₂)x₂x₁y=f(x)Oxyx₂x₁f(x₁)f(x₂)y=f(x)(1)(2)⒉单调性与单调区间若函数y=f(x)在某个区间是增函数或减函数,则就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间叫做函数y=f(x)的单调区间.此时也说函数y=f(x)是这一区间上的单调函数.在单调区间上,增函数的图象是上升的,减函数的图象是下降的.注意:(1)x₁,x₂是该区间内任意的两个实数,如果忽略任意取值这个条件,就不能保证函数是增函数(或减函数).如例:f(x)=x²在(0,+∞)上为增函数在(-∞,0)上为减函数;但在(-∞,+∞)上不是单调函数.(2)函数的单调区间是其定义域上的子集0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右,图象上升数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右,图象上升数量特征y随x的增大而增大0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右,图象上升从左至右,图象下降数量特征y随x的增大而增大0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右,图象上升从左至右,图象下降数量特征y随x的增大而增大y随x的增大而减小0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右,图象上升从左至右,图象下降数量特征y随x的增大而增大当x1<x2时,f(x1)