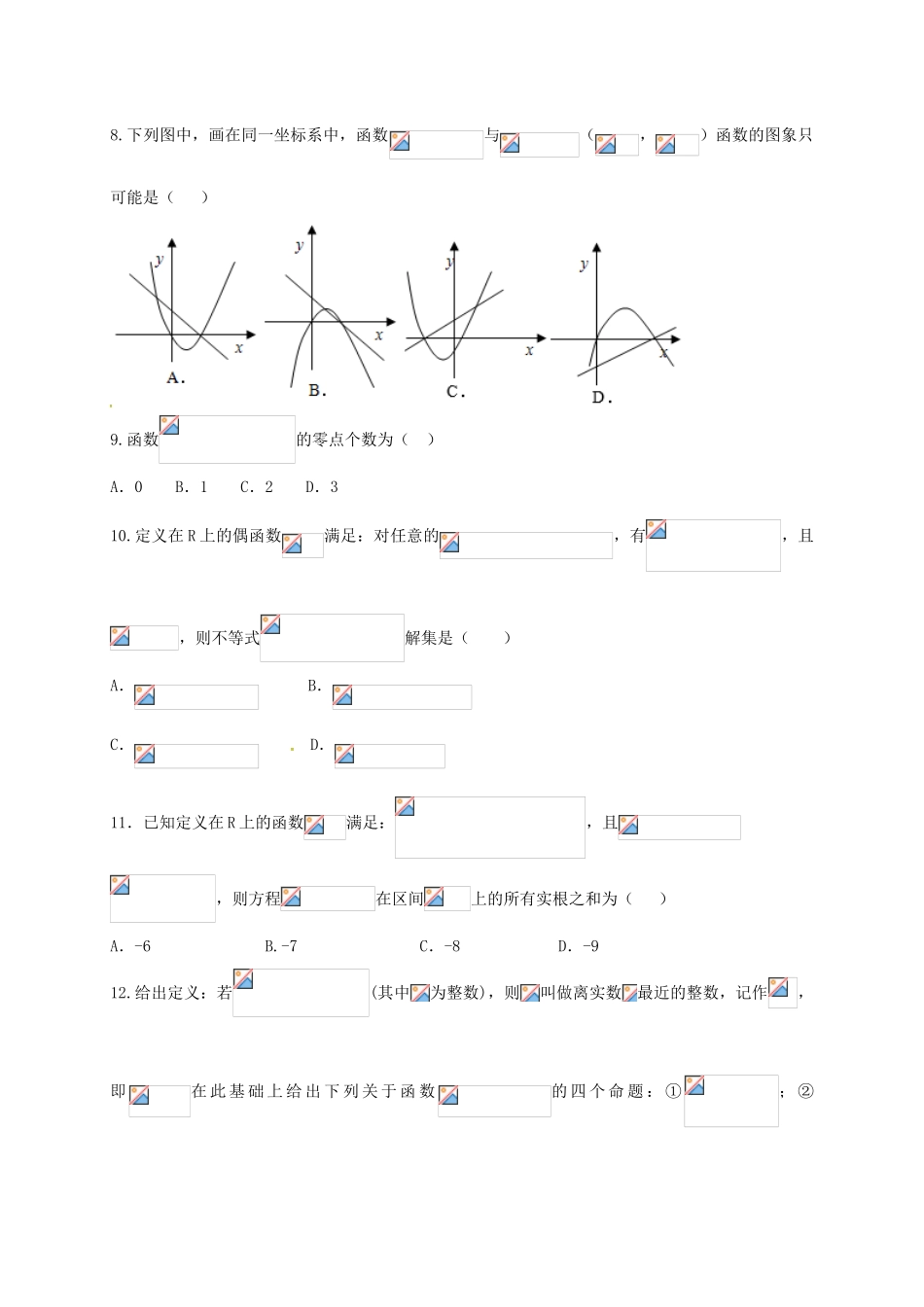
2016-2017学年度上学期(5-15班)期中考试高一年级数学试卷考试时间:120分钟一、选择题:(本题包括12小题,共60分,每小题只有一个选项符合题意)1.已知集合,则下列式子表示不正确的是()A.B.C.D.2.若,,则()A.B.C.D.3.已知映射,在映射下的原象是()A.B.C.D.4.下列函数是同一函数的是()A.B.C.D.5.设函数是定义在上的奇函数,且,当时,,则()A.B.C.D.6.已知,则的大小关系为()A.B.C.D.7.若函数的定义域是[-2,4],则函数的定义域是()A.[-4,4]B.[-2,2]C.[-3,2]D.[2,4]8.下列图中,画在同一坐标系中,函数与(,)函数的图象只可能是()9.函数的零点个数为()A.0B.1C.2D.310.定义在R上的偶函数满足:对任意的,有,且,则不等式解集是()A.B.C.D.11.已知定义在R上的函数满足:,且,则方程在区间上的所有实根之和为()A.-6B.-7C.-8D.-912.给出定义:若(其中为整数),则叫做离实数最近的整数,记作,即在此基础上给出下列关于函数的四个命题:①;②;③;④的定义域是,值域是,则其中真命题的序号是()A.①②B.①③C.②④D.③④二、填空题:(本题包括4小题,共20分)13.设是上的奇函数,当时,(为常数),则____________.14.若为一次函数,且,则.15.已知函数的反函数为,则.16.已知函数,若函数有3个零点,则实数的取值范围是___________.三、解答题:本大题共6小题,共70分.17.(本小题满分10分)计算:(1);(2).18.(本小题满分12分)已知集合(1)当时,求集合,;(2)若,求实数的取值范围.19.(本小题满分12分)设函数,若且对任意实数不等式恒成立.(1)求实数的值;(2)当时,是单调函数,求实数的取值范围.20.(本小题满分12分)已知幂函数在上单调递增.(1)求实数k的值,并写出相应的函数的解析式;(2)对于(1)中的函数,试判断是否存在正数,使函数,在区间上的最大值为5,若存在,求出的值;若不存在,请说明理由.21.(本小题满分12分)已知定义在区间(0,+∞)上的函数f(x)满足,且当x>1时,.(1)求的值;(2)试判断的单调性,并用定义证明;(3)若,求在上的最小值.22.(本小题满分12分)已知定义域为的函数是奇函数.(1)求的值;(2)关于的不等式,对任意恒成立,求取值范围.5-15班期中考试高一年级数学答案一、选择题:(本题包括12小题,共60分,每小题只有一个选项符合题意)BDBBABCBCABB二、填空题:(本题包括4小题,共20分)13.-914.15.216.三、解答题:(本题包括6小题,共70分)17.(1)1(2)6(10分)18.(1)(6分)(2)(6分)19.(1)由题意易得.(5分)(2)由(1)得的图像对称轴方程,再由为单调函数,可得(7分)20.(1)由幂函数的形式及的单调性得(6分)(2)将得,根据一元二次函数的图像和性质得,解得.(6分)21.(1)设(3分)(2)函数在区间上单调递减,证明略:(5分)(3)由于函数在区间上单调递减,所以在时,函数也单调递减,所以当取得最小值,.(4分)22.(1)因为是奇函数,所以,解得,所以又由.(5分)(2)得从而得解得的取值范围为.(7分)