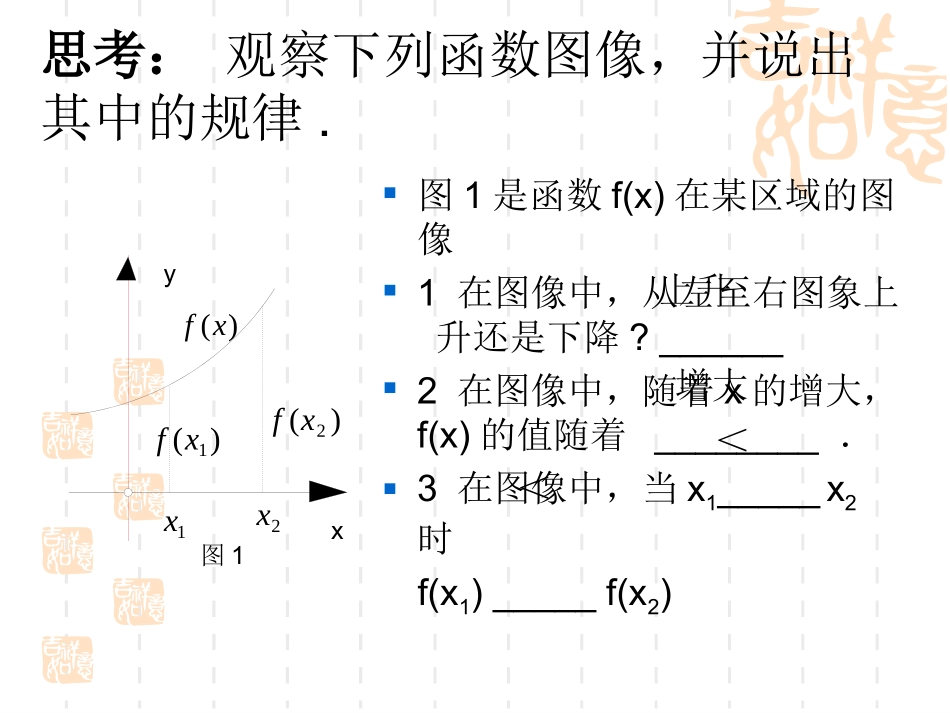
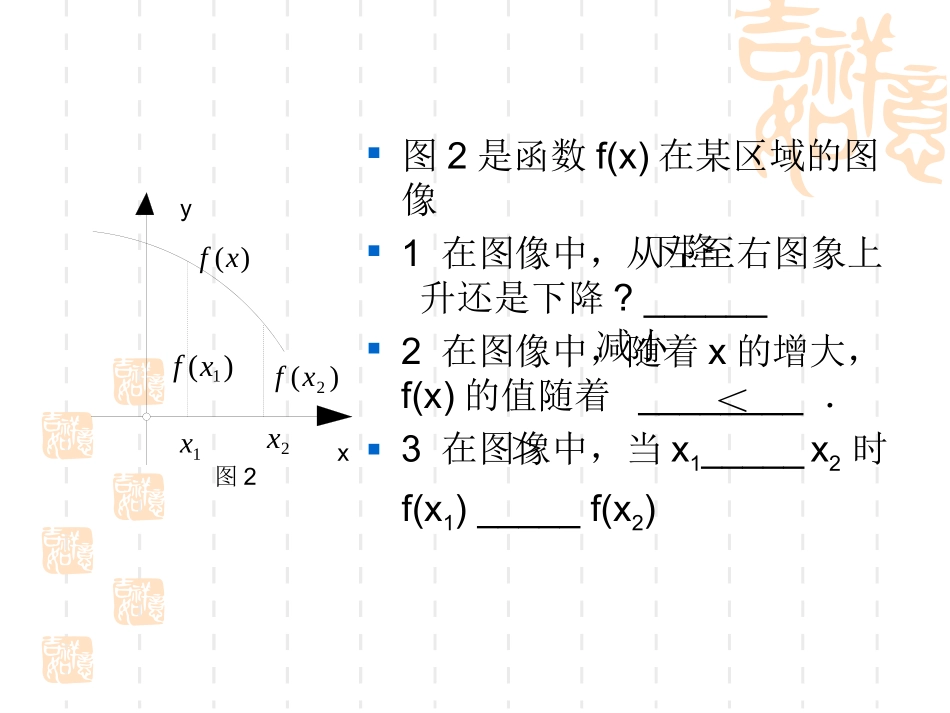
1.3函数的基本性质1.3.1单调性与最大(小)值(1)艺术高中数学组思考:观察下列函数图像,并说出其中的规律.图1是函数f(x)在某区域的图像1在图像中,从左至右图象上升还是下降?______2在图像中,随着x的增大,f(x)的值随着________.3在图像中,当x1_____x2时f(x1)_____f(x2)1x2x)(1xf)(2xf)(xf图1yx上升增大<<图2是函数f(x)在某区域的图像1在图像中,从左至右图象上升还是下降?______2在图像中,随着x的增大,f(x)的值随着________.3在图像中,当x1_____x2时f(x1)_____f(x2)1x2x)(1xf)(2xf)(xf图2yx下降减小<>函数单调性定义1.增函数一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2当x1f(x2),那么就说f(x)在区间D上是减函数.注意:1函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;2必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2)函数的单调性与单调区间如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间:例一:图是定义在闭区间[-5,5]上的函数f(x)的图象,根据图象说出的单调区间,以及在每一单调区间上,函数是增函数还是减函数?解:函数f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中在区间[-5,-2),[1,3)上是减函数,在区间[-2,1),[3,5]上是增函数.531-2-5xOy函数的单调性是对某个区间而言的,对于单独的一点,由于它的函数值是唯一确定的常数,因而没有增减变化,所以不存在单调性问题;中学阶段研究的主要是连续函数或分段连续函数,对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此,在考虑它的单调区间时,包括不包括端点都可以;还要注意,对于在某些点上不连续的函数,单调区间不包括不连续点.例二:证明函数f(x)=3x+2在R上是增函数.证明:设任意x1、x2R∈,且x10,又由x10,于是,即∴在(0,+∞)上是减函数.2112121211xxfxfxxxxxxxf1)(21120xxxx120fxfxxxf1)(练习课本P32页3、4小结:函数的单调性一般是先根据图象判断,再利用定义证明.求函数的单调区间时必须要注意函数的定义域,单调性的证明一般分四步:取值→作差→变形、定号→下结论作业课本P39页2、3