幂函数的图象与性质VIP免费

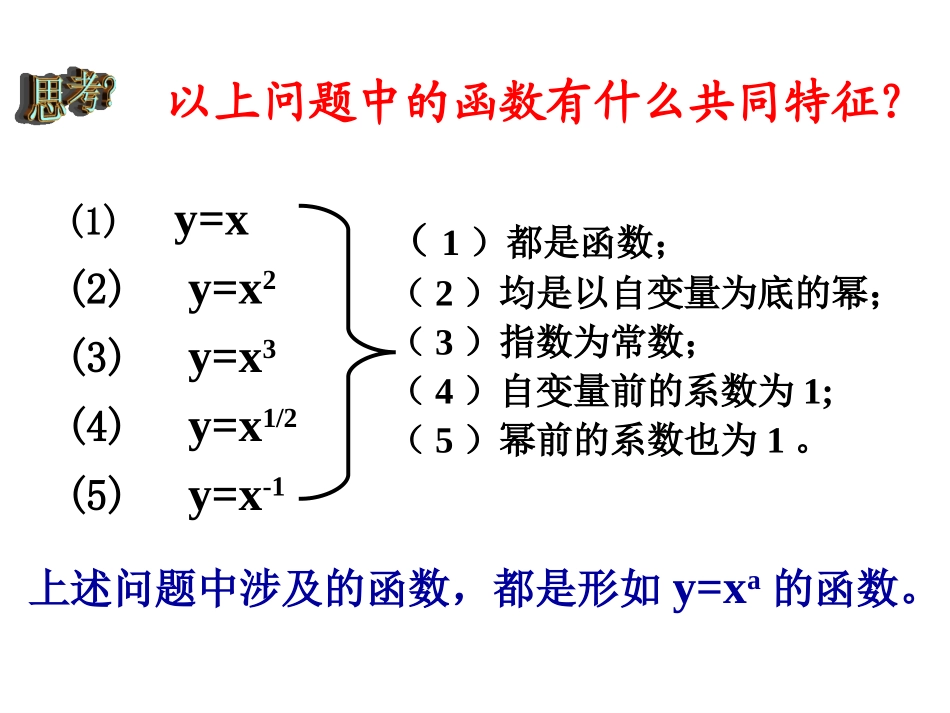
我们先来看看几个具体的问题:(1)如果张红买了每千克1元的蔬菜W千克,那么她需要支付__________P=W元(2)如果正方形的边长为a,那么正方形的面积_____(3)如果立方体的边长为a,那么立方体的体积___________(5)如果某人ts内骑车行进1km,那么他骑车的平均速度_____________p是w的函数S=a²S是a的函数V=a³V是a的函数V=t⁻¹km/sV是t的函数引入课题(4)如果一个正方形场地的面积为S,那么这个正方形的边长_____________12a=Sa是S的函数以上问题中的函数有什么共同特征？（1）都是函数；（2）均是以自变量为底的幂；（3）指数为常数；（4）自变量前的系数为1;（5）幂前的系数也为1。上述问题中涉及的函数，都是形如y=xa的函数。(1)y=x(2)y=x2(3)y=x3(4)y=x1/2(5)y=x-1幂函数的定义幂函数的定义域：一般地，我们把形如y=xa的函数叫做幂函数，其中x是自变量，a是常数。使xa有意义的实数的集合。例1判断下列函数哪些是幂函数：（1）y=5x（2）y=2x（3）y=x0.3（4）y=x+1（5）y=1/x4（6）y=xxx√Xxx√_______2,2.1则这个函数的解析式为），，点（已知某幂函数的图象过例______221412mxmmym则是幂函数，：函数练习自己动手:在同一平面直角坐标系内做出幂函数12312,,,,yxyxyxyxyx的图象4321-1-2-3-4-2246图象如下yx2yx3yx12yx(1,1)从图象能得出他们的性质吗?y=x-1几个幂函数的性质:定义域值域奇偶性单调性公共点yx2yx3yx12yx1yx0y0y0yRRRRR(0,0),(1,1)(0,0),(1,1)(0,0),(1,1)(0,0),(1,1)(1,1)奇函数偶函数非奇非偶奇函数奇函数增函数增函数增函数结论结论函数的图象都通过点（1，1）；函数是奇函数，函数是偶函数；在区间上，函数是增函数，函数是减函数；在第一象限内，函数的图象向上与y轴无限接近，向右与x轴无限接近。12312,,,,yxyxyxyxyx31,,yxyxyx2yx(0,)1232,,,yxyxyxyx1yx1yx幂函数y=xa具有下列性质：（1）a>0时：1.图象都过点（0，0），（1，1）.2.在（0，+∞）上是增函数.（2）a<0时：1.图象都过点（1，1）.2.在（0，+∞）上是减函数.3.在第一象限内，图象向上与y轴无限接近，向右与x轴无限接近.2.()[0,).fxx例证明幂函数在上是增函数1212:,[0,],,xxxx证明任取且则1212121212()()()()ffxxxxxxxxxx1212xxxx12121212,,[0,],0,0,xxxxxxxx因为所以12()(),()[0,].fffxxxx所以即幂函数在上的增函数方法技巧方法技巧::分子有理化分子有理化例例33比较下列各组中两个值的大小，并说明理由：比较下列各组中两个值的大小，并说明理由：433.2434.25631.05635.023)2(23)3(.小结小结形如的函数叫做幂函数，其中x是自变量，a是常数。ayx5种常见幂函数的图象特征及函数性质。12312,,,,yxyxyxyxyx利用幂函数性质简单的判断大小关系。