正弦余弦函数图像VIP免费

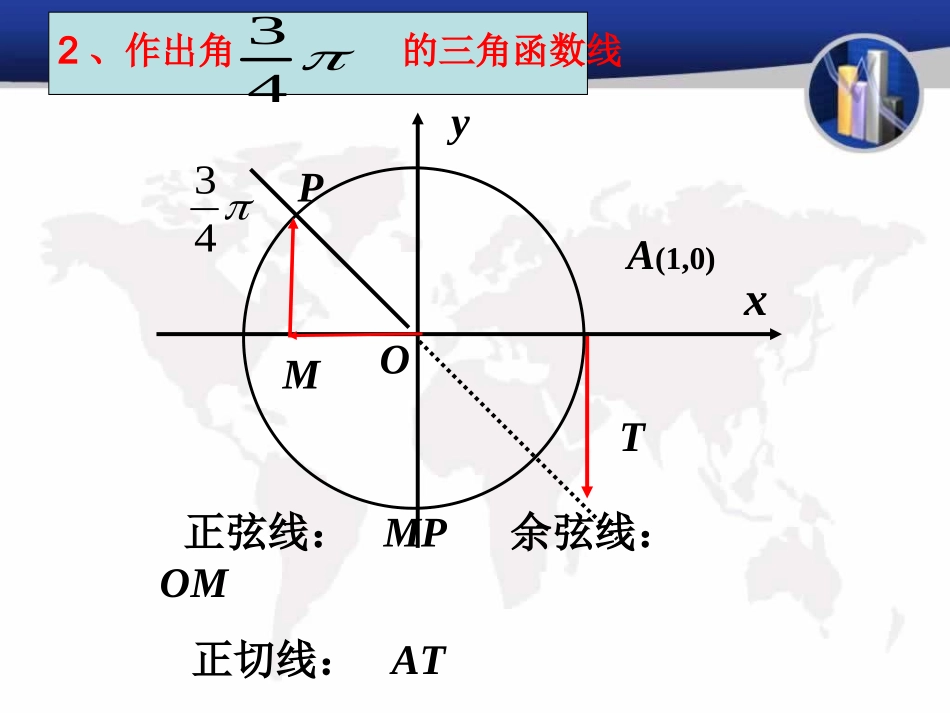
1.4.11.4.1正弦函数、余弦函数的图象正弦函数、余弦函数的图象)()(axfyxfy图像经过怎样的平移?)(axfy1、问题思考：设实数a>0，知识复习：PxyOA(1,0)T正弦线：MP余弦线：OM正切线：ATM432、作出角的三角函数线43作正弦函数的图象xyo1-12BO1y=sinx,x[0,2]2探究新知23思考：y=sinx，x[2,4)的图象与y=sinx，x[0,2)的图象形状上有何特点？原因？相同.函数值重复出现.探究新知如何作y=sinx，xR的图象？y=sinx，x[0,2)的图象向左、右平移（每次2个长度单位）.探究新知xyo1-1-2-234探究新知y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-π探究新知函数y=sinx，x∈R的图象叫做正弦曲线y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-π形成结论y=cosx的图象画法思考:y=cosx和y=sin(x+)有怎样的关系？2探究新知正弦曲线向左平移个长度单位而得.2y=cosx，xR的图象叫余弦曲线.探究新知xyO1-1222222222222在函数y=sinx，x∈[0，2π]的图象上，起关键作用的点有哪几个？x-1O2ππ1y探究新知223思考：若用列表描点画y=sinx，x[0,2]的草图，抓哪些关键的点？,0)(2,,-123π,π,0,,12π,0,0探究新知函数y=cosx，x∈[0，2π]的图象如何？其中起关键作用的点有哪几个？xyO2ππ122-1探究新知思考：若用列表描点画y=cosx，x[0,2]的草图，抓哪些关键的点？,1)(2,,023π,π,-1,,02π,0,1探究新知典例讲评例1用“五点法”画出下列函数的简图：(1)y=1+sinx，x∈[0，2π]；(2)y=-cosx，x∈[0，2π].x-1O2ππ2p32p1y2y=1+sinx典例讲评的交点个数是多少？与函数函数21])2,2[(1sinyxxyxcosx-cosx102p32pp2p1001-1-100-1x-1O2ππ2p32p1yy=-cosx上的函数图像在区间函数练习：利用五点法画出],0[2cosxy