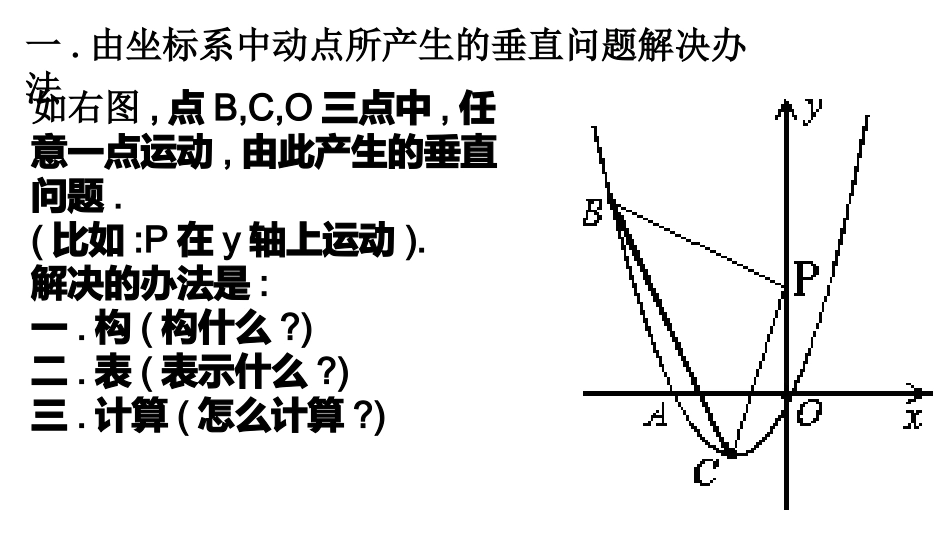
二次函数压轴题小结油田八中景金安一.由坐标系中动点所产生的垂直问题解决办法如右图,点B,C,O三点中,任意一点运动,由此产生的垂直问题.(比如:P在y轴上运动).解决的办法是:一.构(构什么?)二.表(表示什么?)三.计算(怎么计算?)1.已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C(1)求抛物线的解析式.(2)P是y轴上的一个动点.当∠BPC=900时,求P的坐标.(3)Q是抛物线第一象限内的一个动点,当BQBC⊥是,求点Q的坐标.二.平面直角坐标系中的相似三角形问题的解决办法.如右图,P在抛物线上运动,PDx⊥轴于D△CPD与△ABO相似一.分(怎么分情况?)二.表三.计算想一想,分是为了什么?2.直线y=x+4与坐标轴分别交于A,B两点,过A,B两点的抛物线为y=-x2+bx+c.点D为线段AB上一动点,过点D作CDx⊥轴于点C,交抛物线于点E.(1)求抛物线的解析式(2)连结BE,当△BDE与△ADC相似时,求点D的坐标.三.运动中产生的平行四边形问题的解决方法.一.分二表三计算.关键在于分情况.如右图,A,P是定点,M,N是x轴及抛物线上的点,要使以APNM四点为顶点的四边形为平行四边形,求M的坐标.抓着定线段AP作文章.若AP是对角线.由AM//NP可得两个点.若AP是边,抓着MN//AP作文章.思考:如何实现MN//AP且MN=AP(特别是倾斜的时候?)3.已知抛物线y=ax2-2ax+c交y轴于C,交x轴于A(-1,0),B两点,且OC=3OA.(1)求抛物线及直线BC的解析式.(2)P在直线BC上,P的横坐标为1.M是x轴上的一点,N是抛物线上一点,当以APMN为顶点的四边形为平行四边形时,求M的坐标.四.面积问题1.由动点产生的三角形的面积,可利用分割法来计算的.P是抛物线上的一个动点时,利用点P的横坐标来表示△BCP的面积.利用分割法,如何分割?类比变化:求四边形OCPB的面积呢?4.y=ax2-x+c交x轴于A(-1,0),B.直线y=kx+1.5过点A,交抛物线于另一点D,且D的横坐标为2.(1)抛物线及直线的解析式.(2)P是抛物线在直线AD下方的一个动点,在点P移动的过程中,求△ADP的面积的最大值.2.面积一定的时候,不定点坐标的求法.要点既要全面考虑,又要学会删除不合乎要求的情况.如右图,抛物线的顶点坐标为(m,n),P在抛物线上一点,且△ABP和△ADP由于△OBC的面积一定,因此△ABP的面积也是一定的.它的面积的变化是由于P的位置的变化引起的.如何考虑,才能够不落下点,又能排除不合理的点?5.y=ax2+bx-4交x轴于A(1,0),B(4,0)交y轴于点C.(1)求抛物线的解析式(2)P是抛物线上的一个点,且△ABP的面积和△BCO的面积的比等于3:4,求点P的坐标.五.其他二次函数压轴题,可以说变化无穷.但是,其他的一切变化,大致都能找到以典型问题的痕迹.最终都要归一相似三角形,解直角三角形,方程都基本的数学思想中去.下面举几个例子.6.y=ax2+bx+4交x轴于A(2,0),C,交y轴于B,且CO=2AO(1)求抛物线的解析式.(2)P是抛物线上一个点,且AP平分∠BAO,求点P的坐标.7.y=ax2+bx-4经过A(-8,0),B(2,0)两点,直线x=-4交x轴于点C,交抛物线于点D.(1)求该抛物线的解析式;(2)点P在抛物线上,点E在直线x=-4上,若以A,O,E,P为顶点的四边形是平行四边形,求点P的坐标;(3)若B,D,C三点到同一条直线的距离分别是d1,d2,d3,且满足d3=2d1=2d2.这样的直线是否存在?若存在,直接写出的值d3,若不存在,说明理由.