函数的单调性VIP免费

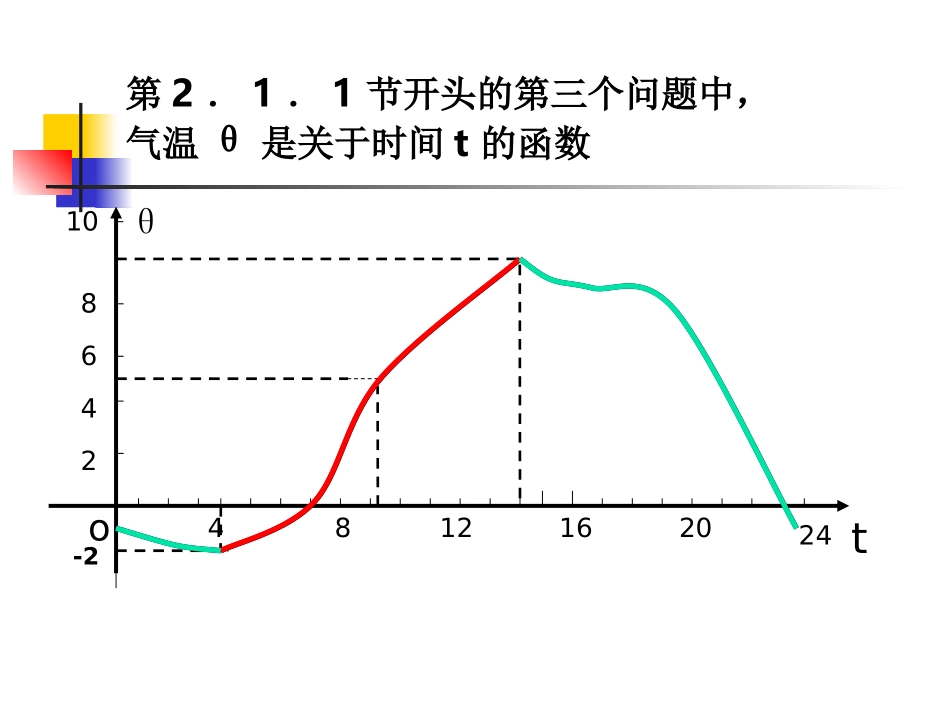
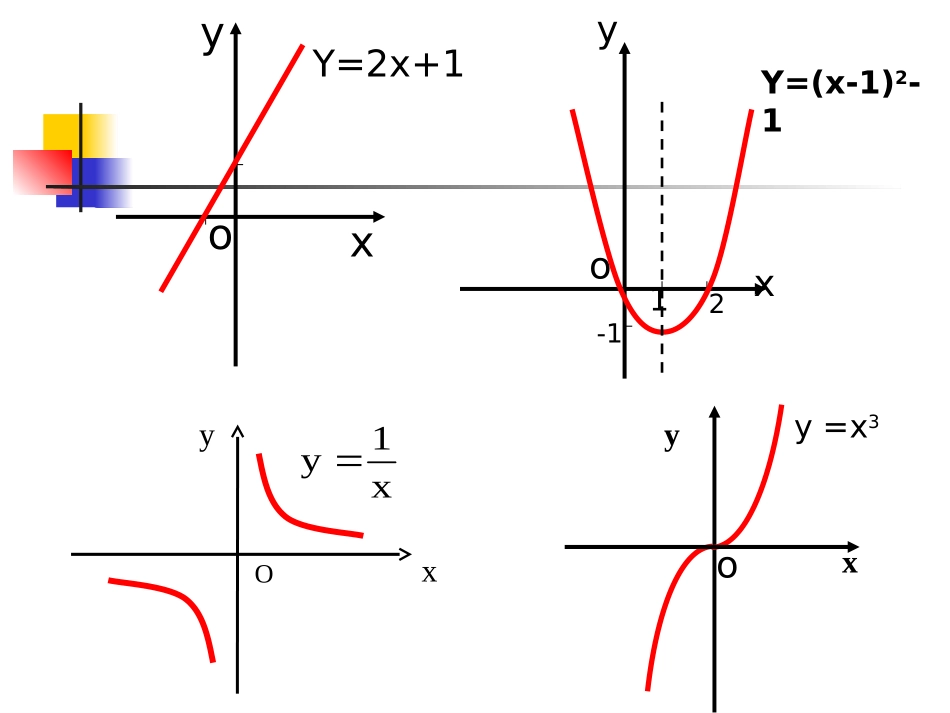
长沙市工读学校θ第2．1．1节开头的第三个问题中，气温θ是关于时间t的函数4812162024to-2248610xyoyY=2x+1xoY=(x-1)2-112-1yxy=x3oyOxx1yOxyx()fx2()fxxOxyx()fx2()fxxxOxyx()fx2()fxxOxyx()fx2()fxxOxyx()fx2()fxxOxyx()fx2()fxxOxyx()fx2()fxxOxyx()fx2()fxxOx()fxxy2()fxxxyOx()fx2()fxx（-∞，0]上随x的增大而减小()fx[0，+∞）上随x的增大而增大()fxxyo)(xfymnf（x1）x1x2f（x2）如果对于区间I内的任意两个值1212,,xxxx当时12()()fxfx都有那么就说在区间I上是单调增函数()yfxI称为的单调增区间()yfxf（x1）x1x2f（x2）如果对于区间I内的任意两个值1212,,xxxx当时12()()fxfx都有那么就说在区间I上是单调减函数()yfxI称为的单调减区间()yfx)x(fyOxyyxoyY=2x+1xoY=(x-1)2-112-1yxy=x3oyOxx1y增区间为(,)增区间为增区间为(,)[1,)减区间为(,1]减区间为(,0),(0,)例1:写出函数的单调区间（1）函数的单调性也叫函数的增减性；（2）函数的单调性是对某个区间而言的，它是个局部概念。这个区间是定义域的子集。（3）单调区间：针对自变量x而言的。若函数在此区间上是增函数，则区间为单调递增区间若函数在此区间上是减函数，则区间为单调递减区间例2:证明：函数f(x)=3x+2在R上是单调增函数。证明：设x1，x2是R上的任意两个值，且x1＜x2，则f(x1)－f(x2)=（3x1+2）－（3x2+2）=3（x1－x2）∵x1＜x2，∴x1－x2<0∴f(x1)－f(x2)<0即f(x1)