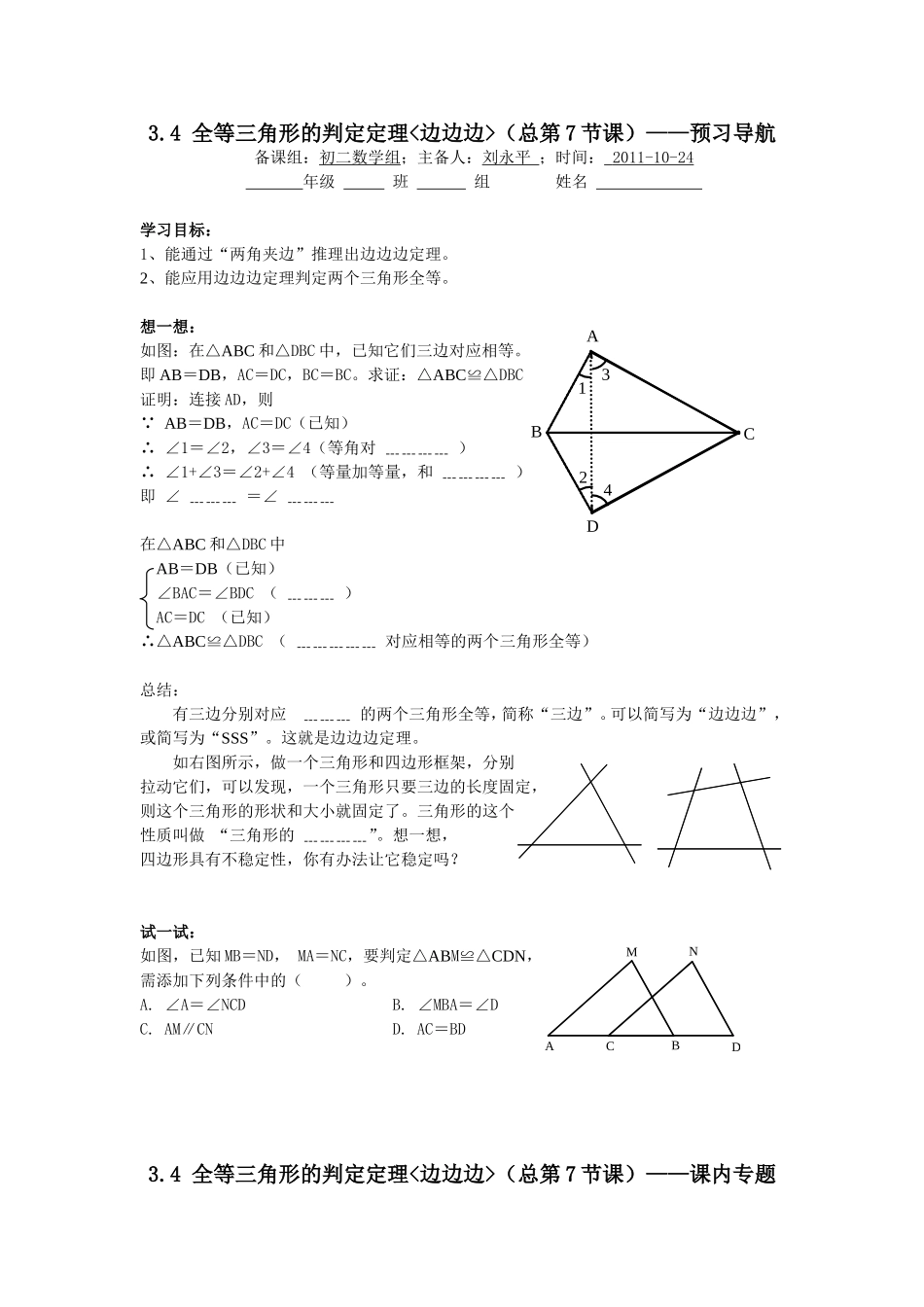
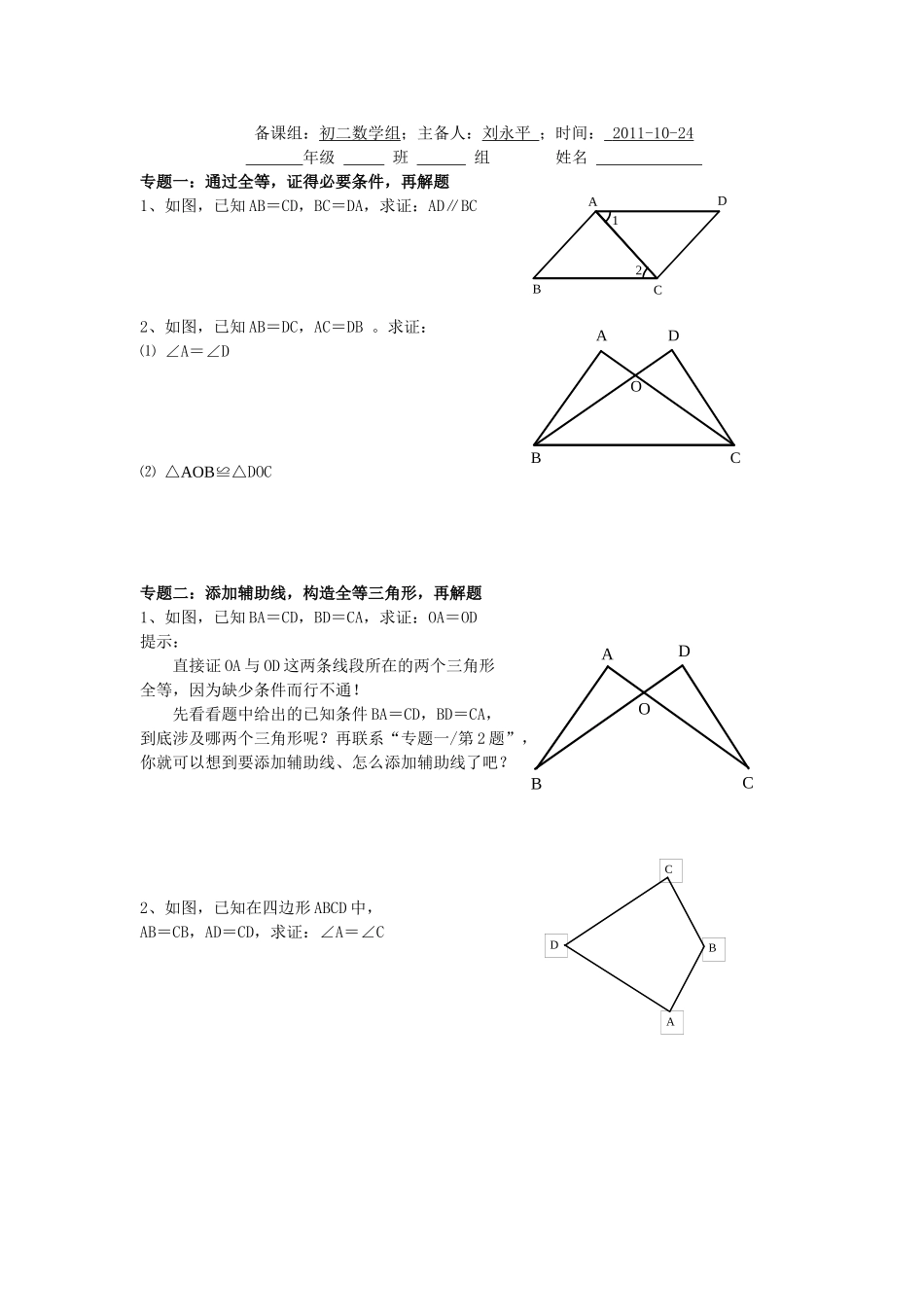
A3CD4B12DNABCM3.4全等三角形的判定定理<边边边>(总第7节课)——预习导航备课组:初二数学组;主备人:刘永平;时间:2011-10-24年级班组姓名学习目标:1、能通过“两角夹边”推理出边边边定理。2、能应用边边边定理判定两个三角形全等。想一想:如图:在△ABC和△DBC中,已知它们三边对应相等。即AB=DB,AC=DC,BC=BC。求证:△ABC≌△DBC证明:连接AD,则∵AB=DB,AC=DC(已知)∴∠1=∠2,∠3=∠4(等角对﹍﹍﹍﹍)∴∠1+∠3=∠2+∠4(等量加等量,和﹍﹍﹍﹍)即∠﹍﹍﹍=∠﹍﹍﹍在△ABC和△DBC中AB=DB(已知)∠BAC=∠BDC(﹍﹍﹍)AC=DC(已知)∴△ABC≌△DBC(﹍﹍﹍﹍﹍对应相等的两个三角形全等)总结:有三边分别对应﹍﹍﹍的两个三角形全等,简称“三边”。可以简写为“边边边”,或简写为“SSS”。这就是边边边定理。如右图所示,做一个三角形和四边形框架,分别拉动它们,可以发现,一个三角形只要三边的长度固定,则这个三角形的形状和大小就固定了。三角形的这个性质叫做“三角形的﹍﹍﹍﹍”。想一想,四边形具有不稳定性,你有办法让它稳定吗?试一试:如图,已知MB=ND,MA=NC,要判定△ABM≌△CDN,需添加下列条件中的()。A.∠A=∠NCDB.∠MBA=∠DC.AM∥CND.AC=BD3.4全等三角形的判定定理<边边边>(总第7节课)——课内专题12ABCDDOABCABCODDCBA备课组:初二数学组;主备人:刘永平;时间:2011-10-24年级班组姓名专题一:通过全等,证得必要条件,再解题1、如图,已知AB=CD,BC=DA,求证:AD∥BC2、如图,已知AB=DC,AC=DB。求证:⑴∠A=∠D⑵△AOB≌△DOC专题二:添加辅助线,构造全等三角形,再解题1、如图,已知BA=CD,BD=CA,求证:OA=OD提示:直接证OA与OD这两条线段所在的两个三角形全等,因为缺少条件而行不通!先看看题中给出的已知条件BA=CD,BD=CA,到底涉及哪两个三角形呢?再联系“专题一/第2题”,你就可以想到要添加辅助线、怎么添加辅助线了吧?2、如图,已知在四边形ABCD中,AB=CB,AD=CD,求证:∠A=∠C