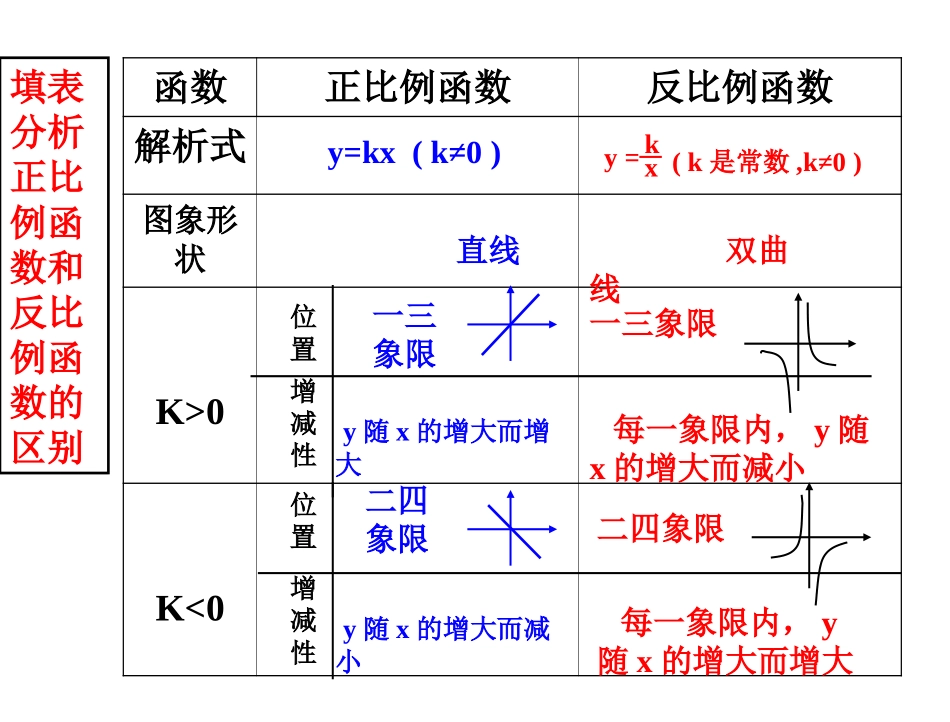
二四象限一三象限函数正比例函数反比例函数解析式图象形状K>0K<0位置增减性位置增减性y=kx(k≠0)(k是常数,k≠0)y=xk直线双曲线y随x的增大而增大一三象限每一象限内,y随x的增大而减小二四象限y随x的增大而减小每一象限内,y随x的增大而增大填表分析正比例函数和反比例函数的区别知识点1反比例函数的性质(重难点)y2),(x3,y3),其中x10,∴函数图象在第一、三象限. x10. k>0时,在每个象限内y随x的增大而减小,∴y2-2C.m>2)B.m<-2D.m<2解析:反比例函数在其象限内y的值随x值的增大而增大,则需要m+2<0,所以m<-2.2、如图,是反比例函数的图象的一支.(1)函数图象的另一支在第几象限?(2)求常数m的取值范围。(3)点A(-3,y1)(-1,y2),(2,y3)都在这个反比例函数的图象上,比较y1、y2、y3的大小。Oxyxmy2图象的一个分支,对于给出的下列说法:图26-1-34.(2012年山东济宁)如图2613,是反比例函数y=k-2x的①常数k的取值范围是k>2;②另一个分支在第三象限;③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;④在函数图象的某一个分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2.其中正确的是__________(在横线上填出正确的序号).①②④知识点2k的几何意义(知识拓展)【例2】过如图26-1-4所示双曲线上任一点P作x轴、y轴的垂线PM、PN,求四边形PMON的面积.图26-1-4解:依题意设函数解析式为y=kx(k<0),P(x,y). PM⊥x轴,∴△PMO是直角三角形,且OM=|x|,PM=|y|.∴S△PMO=12OM·PM=12|x||y|=12|xy|.又由y=kx,有k=xy,∴S△PMO=12|k|.同理,可得S△PNO=12|k|.∴S四边形PMON=S△PMO+S△PNO=12|k|+12|k|=|k|.若P在第四象限,或双曲线在第一、三象限,则同样有S四边形PMON=|k|.因此k的几何意义为:过双曲线上任意一点作x轴、y轴的垂线,所得的四边形的面积为|k|.【例2】如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是.xyoMNpx3yPDoyx1、如图,点P是反比例函数图象上的一点,PD⊥x轴于D.则△POD的面积为.xy2(m,n)1S△POD=OD·PD=mn mn=2,∴S△POD=12121A.__,,,,,,,,,,,,,,,)0(1,.4321111111则有面积分别为的记边结三点轴于交轴引垂线经过三点分别向的图像上有三点在如图SSSOCCOBBOAAOCOBOACBAxxCBAxxyA.S1=S2=S3B.S1S2>S3BA1oyxACB1C1S1S3S2图26-1-5为此图象上的一动点,过点A分别作AB⊥x轴和AC⊥y轴,垂足分别为B,C,则四边形OBAC周长的最小值为()A.4B.3C.2D.1解析:要使四边形的周长最小,则需要四边形为正方形,此时OB=AB=AC=OC=1,所以周长为4.5.如图2615为反比例函数y=1x在第一象限的图象,点AA知识点三:一次函数与反比例函数例3、如图,一次函数y=kx+b的图象与反比例函数xmy的图象交于A(-2,1)、B(1,n)两点(1)求反比例函数和一次函数的解析式(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围。的图象交于点M(a,1),MN⊥x轴于点N(如图26-1-6),若△OMN的面积等于2,求这两个函数的解析式.图26-1-66.已知:正比例函数y=k1x的图象与反比例函数y=k2x(x>0)跟踪训练解: MN⊥x轴,点M(a,1),∴S△OMN=12a=2,∴a=4....