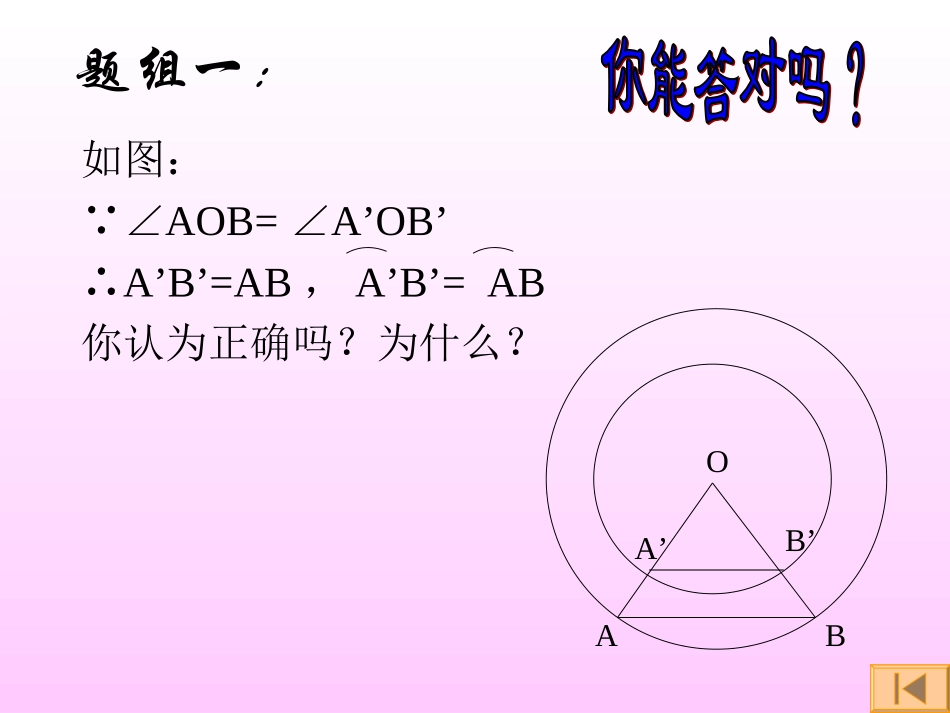
圆心角、弧、弦、弦心距之间的关系一、定义1、圆心角:顶点在圆心的角。二、定理在同圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。2、弦心距:圆心到弦的距离。三、推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量也分别相等。AOBMA′B′M′或等圆圆心角、弧、弦、弦心距之间的关系题组题组22题组一:如图:∵∠AOB=A’OB’∠∴A’B’=AB,A’B’=AB你认为正确吗?为什么?OA’B’AB定理:条件:在同圆或等圆中圆心角相等结论:圆心角所对弦的弦心距相等圆心角所对的弦相等圆心角所对的弧相等条件:在同圆或等圆中圆心角相等条件:在同圆或等圆中圆心角所对的弧相等条件:在同圆或等圆中圆心角相等结论:圆心角所对弦的弦心距相等圆心角所对的弦相等圆心角所对的弧相等结论:圆心角所对弦的弦心距相等圆心角所对的弦相等圆心角相等结论:圆心角所对弦的弦心距相等圆心角所对的弦相等圆心角所对的弧相等命题一:命题二:命题三:题组二:已知:如图AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,请根据所学内容填空:(1)如果AB=CD,那么、、。(2)如果OE=OF,那么、、。(3)如果,那么、、。(4)如果,那么、、。(5)要证AB=CD,必须有或或条件。OE=OFAB=CD∠AOB=COD∠AB=CDAB=CD∠AOB=COD∠AB=CDOE=OFAB=CD∠AOB=COD∠∠AOB=COD∠AB=CDOE=OFAB=CDOE=OFAB=CD∠AOB=COD∠BAECFDO例1:如图点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D求证:AB=CD证明:作OMAB⊥,ONCD⊥,MN分别为垂足。∠MPO=NPO∠OMAB⊥ONCD⊥OM=ONAB=CDPEFOBDACNM拓展性练习:若P点在⊙O上或⊙O内,AB=CD成立吗?请证明:BPD(C)(A)OPACBDO课堂小结1、本节课我们运用旋转变换的思想得到圆的旋转不变性。2、利用圆的旋转不变性学习了定理及推论。3、应用定理和推论时,圆心到弦的垂线段是常用的辅助线。思考题•已知AB和CD是⊙O的两条弦,OM和ON分别是AB和CD的弦心距,如果AB>CD,那么OM和ON有什么关系?为什么?OABCDMN