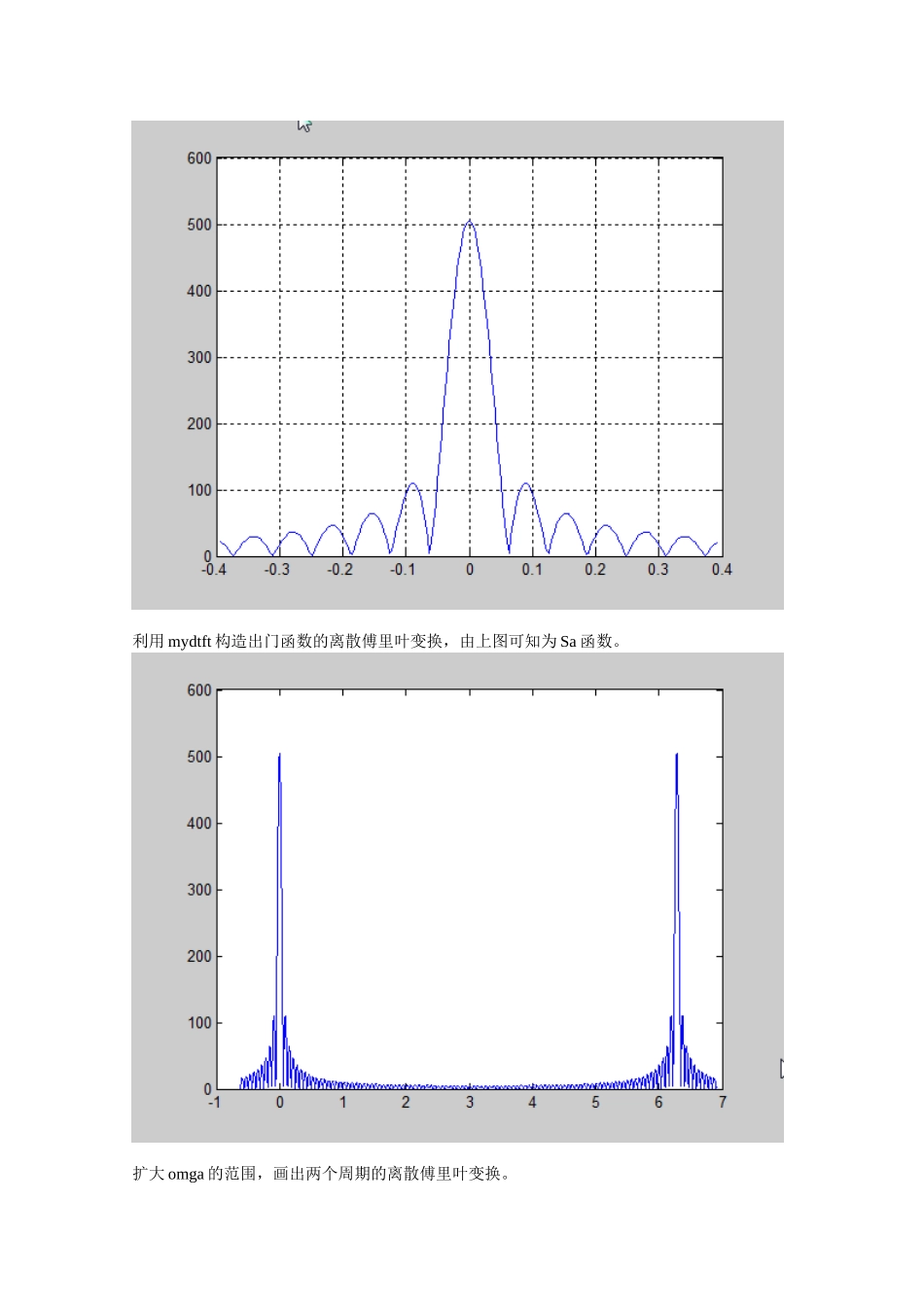
一、实验目的1.自行编写功能函数实现DTFT的变化,并运用该函数实现之后的功能。2.利用编写的DTFT函数,观察函数的离散傅里叶变换,并在三维空间中观察函数的频响特性。3.利用MATLAB设计奇对称系统观察群延时对输入信号的影响。二、实验条件PC机,MATLAB7.0三、实验内容1)编写功能函数mydtft。根据公式,将h[n]用样值向量h和位置向量n描述,则DTFT可以用一个向量和一个矩阵的相乘来实现。函数如下:functionH=mydtft(h,omga)L=length(h);n=[0:L-1]';M=exp(-1i*n*omga);H=h*M;2)做出DTFT,由于MATLAB无法计算连续变量,只能在某个区间范围内将omga赋值为很密的、长度很长的向量来近似为连续变量。由可知,当fs够高时,h[n]可近似于h(t)。fs=50;T=2;A=5;P=2*pi/fs/40;omga=-pi/8:P:pi/8;s=[zeros(1,fs),A*ones(1,floor(T*fs)+1)];%构造门函数S=mydtft(s,omga);plot(omga,abs(S));gridon;figureplot3(omga,real(S),imag(S));gridon;figureP=2*pi/fs/40;omga=-0.2*pi:P:pi*2.2;S=mydtft(s,omga);plot(omga,abs(S));figuresd=[s,s,s];S=mydtft(sd,omga);stem(omga,abs(S));gridon;figure利用mydtft构造出门函数的离散傅里叶变换,由上图可知为Sa函数。扩大omga的范围,画出两个周期的离散傅里叶变换。通过三维空间将幅频特性和相频特性同时放在实轴和虚轴上观察其变化。XY轴的图像——实部频谱函数图XZ轴图像——虚部频谱函数图降低fs,用stem可看出h[n]的离散傅里叶变化。3)N=2000;P=2*pi/N;omga=0:P:pi/3;phi1=-10*omga;phi2=-60*(omga+pi/3);phi3=-30*(omga+pi*2/3);phi=[phi1,phi2,phi3];mag=[ones(1,length(phi)*2/3),zeros(1,length(phi)/3)];%幅度H=mag.*exp(1i*phi);%传递函数h=real(ifft([H,fliplr(conj(H))]));%将函数做共轭然后翻转变成奇对称n=0:100;x=[cos(pi/2*n),cos(pi/4*n)];y=filter(h,1,x);subplot(211);plot(x);subplot(212),plot(y);通过图像可以看出信号延迟了60个单位,并且在中央的波形是因为两信号混叠所产生的。由图也可以看出,有用信号通过滤波器后,允许有一定的延时,但不希望波形失真。为了得到无失真传输,确保相位失真的唯一办法是使不同频率的信号通过滤波器时有相同的延迟。四、实验结论和讨论1.通过设计DTFT函数,更加深入的了解离散时间的傅里叶变换,以及在MATLAB中通过增加取值的密度来用DTFT表现出连续时间的傅里叶变换。2.通过在三维空间将幅频特性和相频特性同时放在实轴和虚轴上观察变化,让我更直观的认识到频响特性的相关性质。3.在这次关于群时延的实验中,通过图像直观的观察到了输入信号经过滤波器后产生的群延时,同时我认识到了自己知识储备的不足,对于许多基础知识以及关于相位失真的知识认识的不扎实。在做关于群延时的实验时有许多模糊和不清楚的地方,当看到老师写的程序是才有些明白该怎么做。