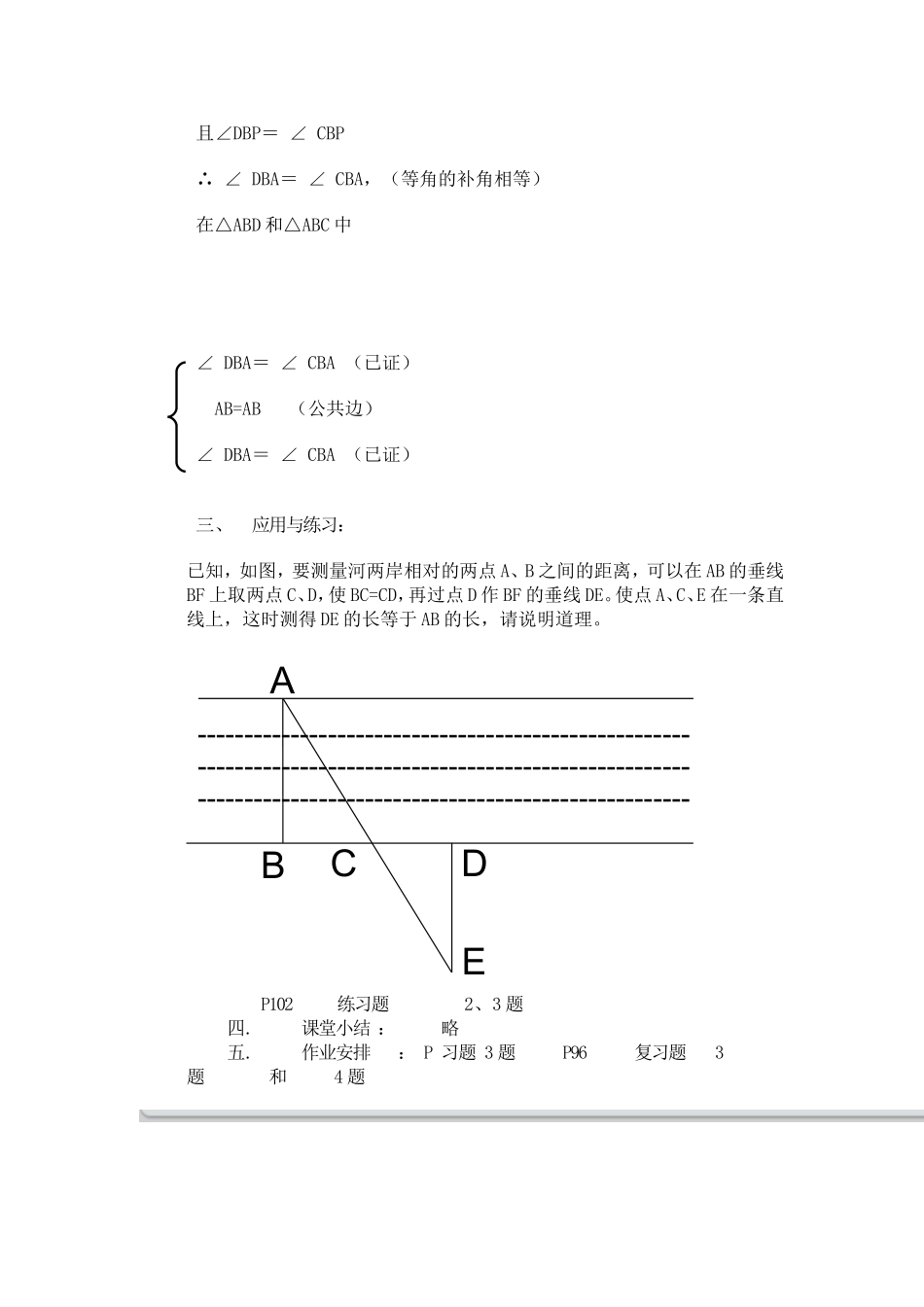
《全等三角形的判定之角边角》——修利萍教学目标:1、知识目标:掌握“角边角”条件的内容,并能初步应用“角边角”条件判定两个三角形全等。2、能力目标:经历探索三角形全等条件的过程,体会如何探索研究问题,让学生初步体会分类思想,提高分析问题和解决问题的能力。3、思想目标:通过画图比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。教学重点:掌握三角形全等的判定方法——“角边角公理”。教学难点:(1)理解“两角一边”分别对应相等的三角形一定会全等,熟练运用“角边角”及"角角边"判定方法(2)运用“角边角公理”证明三角形全等.教学过程:一、新课引入(一)用三角形复原实际问题来引(二)复习旧知全等三角形全等的判定方法一当两个三角形的两边及其夹角分别对应相等时,两个三角形一定全等当两个三角形的两边及其中一边的对角分别对应相等时,两个三角形未必一定全等.即存在边角边定理而不存在边边角定理.二、新课讲解1、想想猜猜如上图,小明不慎把一块三角形的玻璃打碎成两块。试问:小明应该带哪一块碎片到商店去才能配一块与原来一样的三角形玻璃呢?2、做一做(按提示步骤)ⅠⅡ画几个三角形,使它的两个内角分别为45°和60°,且使这两个角的夹边为5厘米.步骤:(1)画一线段AB使它等于5cm(2)画∠MAB=45°(3)在45°角的同侧画∠NBA=60°(4)AM与BN交于点C△ABC就是所作的三角形同法可作△A´B´C´让学生把自己所画的图形进行比较讨论,两个三角形是否全等?2、得出结论判定三角形全等的又一种方法---角边角:如果两个三角形有两角及其夹边分别对应相等,那么这两个三角形全等.简记为ASA(或角边角).几何语言:例1:已知:如图,AB=A’C,∠A=∠A’,∠B=∠C求证:△ABE≌△A’CD证明:在△ABC与△A´B´C´中,CDA'ABE∠A=∠A´AB=A´B´∠B=∠B´∴△ABC≌△A´B´C´(ASA)例2:已知:如图,∠DAB=∠CAB,∠DBP=∠CBP。求证:DB=CB证明:∵∠DBA与∠DBP互为邻补角∠ABC与∠CBP互为邻补角且∠DBP=∠CBP∴∠DBA=∠CBA,(等角的补角相等)在△ABD和△ABC中∠DBA=∠CBA(已证)AB=AB(公共边)∠DBA=∠CBA(已证)三、应用与练习:已知,如图,要测量河两岸相对的两点A、B之间的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再过点D作BF的垂线DE。使点A、C、E在一条直线上,这时测得DE的长等于AB的长,请说明道理。P102练习题2、3题四.课堂小结:略五.作业安排:P习题3题P96复习题3题和4题---------------------------------------------------------------------------------------------------------------------------------------------------------------ABCDE