正弦余弦函数的性质VIP免费

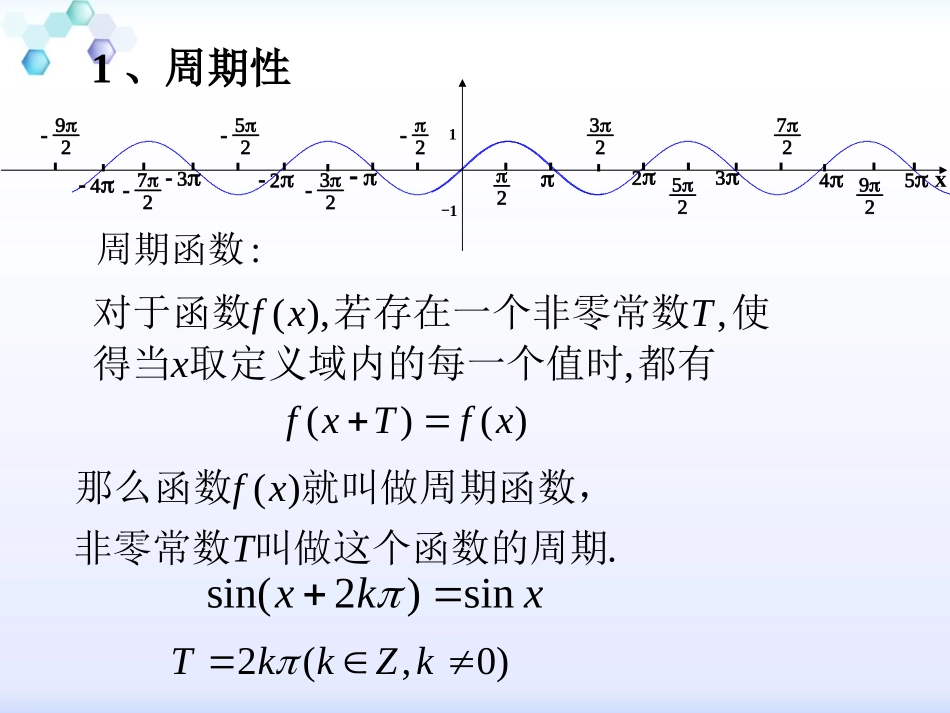
1.4.2正弦、余弦函数的性质（一）X:周期函数都有时取定义域内的每一个值得当使若存在一个非零常数对于函数,,),(xTxf)()(xfTxf.)(叫做这个函数的周期非零常数就叫做周期函数，那么函数Txf1、周期性x1-1xkxsin)2sin()0,(2kZkkT(),().fxfx若在周期函数的所有周期中存在一个最小的正数则这个最小正数就叫做的最小正周期;2,)0,(2,最小正周期是是它的周期都正弦函数是周期函数kZkk.2,)0,(2,最小正周期是是它的周期都余弦函数是周期函数kZkk:1求下列函数的周期例.,都指最小正周期若不加特别说明.,都指最小正周期若不加特别说明;,cos3)1(Rxxy;,2sin)2(Rxxy;),621sin(2)3(Rxxy)0,0.(),sin()4(ARxxAy)0,0.(),cos()0,0.(),sin(ARxxAyARxxAy2Ty=cosx(xR)yo---11-------234--2-3yo---11-------234--2-3••y=sinx(xR)••例2观察图象，写出满足下列条件的x的集合：(1)sinx>0(2)sinx=0(3)sinx<0（4）sin2x>0(5)sin(2x+/3)>0(6)cosx>0(7)cosx=0(8)cosx<0正弦曲线：sinyxxRxy1-1最高点：(2,1)2kkZ最低点：(2,1)2kkZ余弦曲线：cosyxxRxy1-1最高点：(2,1)kkZ最低点：(2,1)kkZ2、最大、最小值例2.求使下列函数取得最大(小)值的x的集合，并写出最大(小)值是多少？(1)y=cosx+1(2)y=-3sin2x(3)y=1-2sinx(4)y=3–5cos2x(5)y=cosx(/6x4/3)x26-12(6)y=cos()[[小结小结]]1.sin(x+),cos(x+)与sinx,cosx一样,最大值最小值都是1、-1，但使函数取得这些值的x值却各不一样；其求法是：换元法。2.注意：cos2x、sin2x[0、1]练习练习：1.下列各等式能否成立？说明理由。(1)2sinx=3(2)sin2x=0.5(3)cosx=-/2(4)sinx+cosx=22.已知sinx=1-2m,则m的取值范围是_________.练习练习:1.(1)函数y=asinx–b的最大值是____________________,最小值是____________________.(2)函数y=asinx+b的最大值是3,最小值是2,则a=__,b=__.2.(1)求f(x)=sin２x-sinx+1的最大值、最小值及相应的x;(2)求f(x)=2cos２x+5sinx-4的最大值、最小值及相应的x；1.4.2正弦、余弦函数的性质（二）正弦、余弦函数的奇偶性、单调性y=sinxyxo--1234-2-31223252722325y=sinx(xR)图象关于原点对称如果对于函数f（x）的定义域内的任意的一个x，都有f（-x）=-f（x）（或f（-x）=f（x）），则称f（x）为这个定义域内的奇函数（或偶函数），奇函数的图象关于原点对称，偶函数的图象关于y轴对称。sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数x6o--12345-2-3-41ycos(-x)=cosx(xR)y=cosx(xR)是偶函数定义域关于原点对称正弦、余弦函数的奇偶性例已知f(x)=ax3+sinx+1，且f(2)=7，则f(-2)=_____.正弦函数的单调性y=sinx(xR)增区间为[，]其值从-1增至122xyo--1234-2-31223252722325减区间为[，]其值从1减至-1223[+2k,+2k],kZ22[+2k,+2k],kZ223余弦函数的单调性y=cosx(xR)增区间为其值从-1增至1[+2k,2k],kZ减区间为，其值从1减至-1[2k,2k+],kZyxo--1234-2-31223252722325例3不通过求值，指出下列各式大于0还是小于0：(1)sin()–sin()1810(2)cos()-cos()523417解：218102又y=sinx在上是增函数]2,2[sin()01810解：5340cos