22.5-二次函数y=ax2-bx-c的图象和性质VIP免费

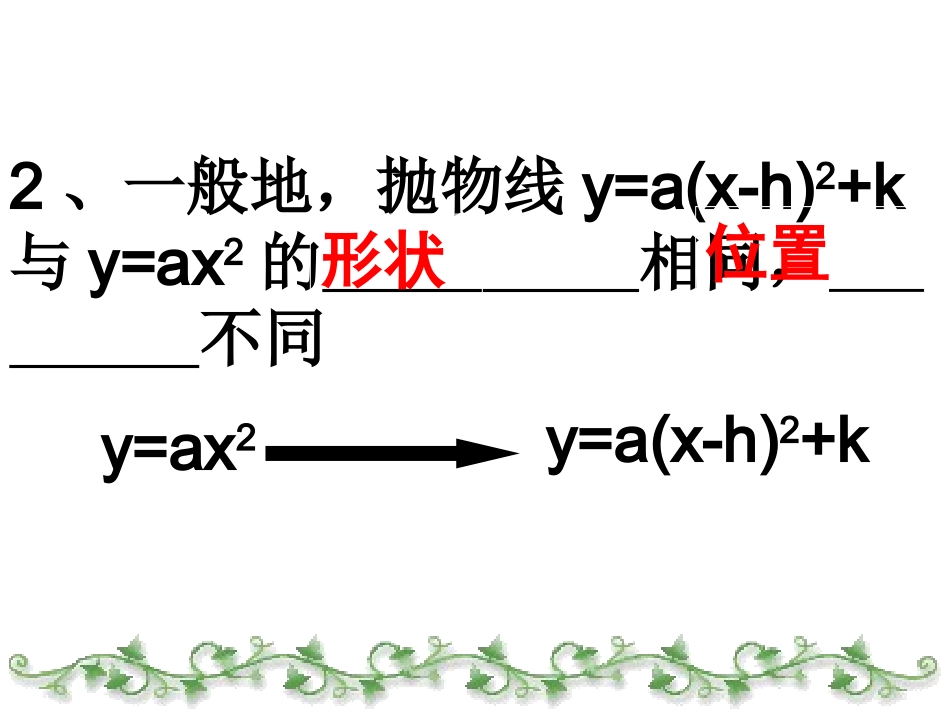
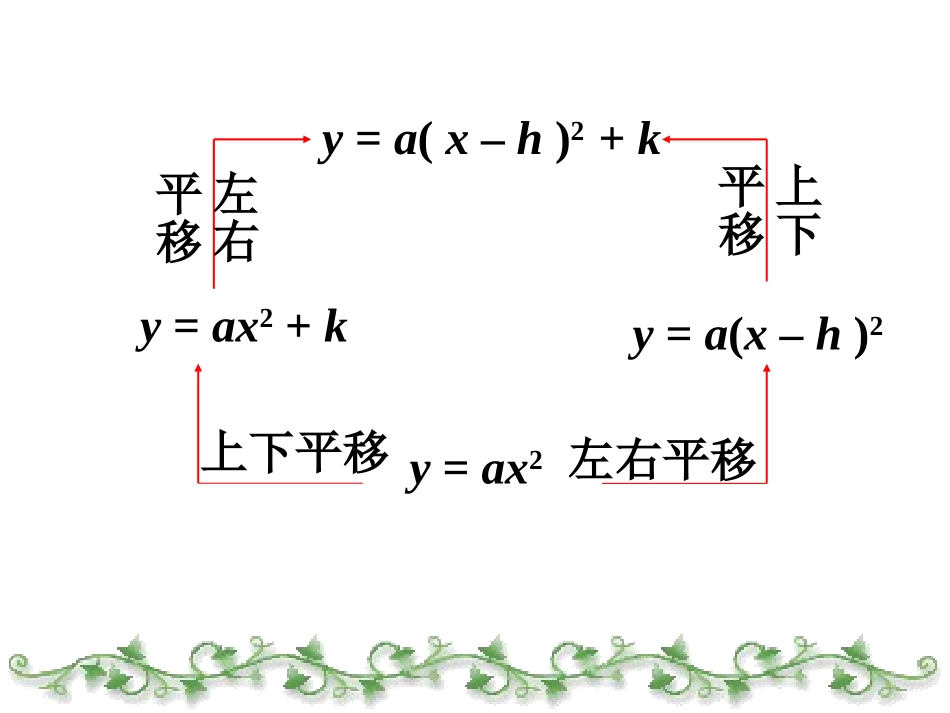
1、抛物线y=a(x-h)2+k的图像与性质：1.当a0﹥时，开口，当a﹤0时，开口，2.对称轴是；3.顶点坐标是。向上向下(h,k)直线X=h2、一般地，抛物线y=a(x-h)2+k与y=ax2的相同，不同y=ax2y=a(x-h)2+k形状位置y=ax2y=ax2+ky=a(x–h)2y=a(x–h)2+k上下平移左右平移上下平移左右平移二次函数开口方向对称轴顶点坐标y=2(x+3)2+5对称轴顶点坐标y=-3x(x-1)2-2y=4(x-3)2+7y=-5(2-x)2-6向上(1,-2)向下向下(3,7)(2,-6)向上直线x=-3直线x=1直线x=3直线x=2(-3,5)标呢？图象的对称轴与顶点坐能否说出二次函数216212xxyy=ax2+bx+c标？图象的对称轴与顶点坐能否说出二次函数21621)1(2xxy标？图象的对称轴与顶点坐能否说出二次函数cbxaxy2)2(一般地，我们可以用配方法求抛物线y=ax2+bx+c(a≠0)的顶点与对称轴y=ax2+bx+ccxabxa)(2cababxa2224)2(cababxa4)2(22abacabxa44)2(221、函数y=ax2+bx+c的图象的顶点坐标:.)44,2(2abacab对称轴:直线abx2函数y=ax2+bx+cⅠ、当a＞0时.:abac442当.abx2最小值=.函数y=ax2+bx+cⅡ、当a＜0时abac442当.abx2最大值=.例1.通过配方，写出下列抛物线的开口方向、对称轴和顶点坐标．（1）y＝2x2＋4x；（2）y＝－2x2－3x；（3）y＝－3x2＋6x－7；（4）y＝x2－4x＋5．2、求下列函数的最大值或最小值：（1）y＝x2－3x＋4；（2）y＝1－2x－x2；（3）y＝；（4）y＝100－5x2；237272xx例2.已知抛物线32bxxy的对称轴是x=2，求b的值。例3.已知二次函数cxxy22的最大值是4，求c的值。例4.已知抛物线y=ax2+bx+c中，，最高点的坐标为，求a、b、c的值。1a25,1练习1、已知抛物线y=ax2+bx+c与抛物线y=-2x2形状相同,且顶点坐标为(1,-5)的函数解析式为.2、若抛物线y＝a(x-m)2+n的图象与函数y＝2x2的图象的形状相同,且顶点为(-3,2),则函数的解析式为.3、已知抛物线y=ax2+bx+c与抛物线y=x2形状相同,但开口方向相反,且顶点坐标为(-1,5)的函数解析式为.例5.已知二次函数3222mxmmxy（1）m当取何值时，函数图象关于y轴对称？（2）m当取何值时，函数图象与y轴交点纵坐标为1？例5.已知二次函数3222mxmmxy（3）m当取何值时，函数最小值为-2？1.抛物线y＝4x2-11x－3与y轴的交点坐标是；与x轴的交点坐标是；2.抛物线y＝-6x2-x+2与y轴的交点坐标是；与x轴的交点坐标是；练习:例6.已知二次函数322xxy1.求它的图象的顶点坐标。2.x取何值时,y随x增大而增大?3.x取何值时,y随x增大而减小?4.x取何值时,y＞0?x取何值时,y＜0?怎样画出函数y=ax2+bx+c的图象?.画二次函数的图象取点时先确定顶点，再在顶点的两旁对称地取相同数量的点，一般取5－7个点即可。例7：用总长为60m的篱笆墙围成矩形场地，矩形面积S随矩形一边长L的变化而变化，当L多少时，场地的面积S最大？?已知直角三角形两条直角边的和等于8，两条直角边各为多少时，这个直角三角形的面积最大，最大值是多少？函数y=ax²+bx+c的图象和性质：顶点坐标：对称轴：开口与y轴交点：与x轴交点：向上向下a>0a>0增减性x>-2abx<-2abx>-2abx<-2ab最值当x=-时，2aby有最小值：4a4ac-b2当x=-时，2aby有最大值：4a4ac-b2直线x=-2ab（0，c）4a4ac-b2-2ab（，）2a-b±b2-4ac（，0）3、已知一次函数y=－2x+c与二次函数y=ax2+bx－4的图象都经过点A(1，－1)，二次函数的对称轴直线是x=－1，请求出一次函数和二次函数的表达式.2、当m=_____时，抛物线y=mx2+2(m+2)x+m+3的对称轴是y轴；当m=_____时，图象与y轴交点的纵坐标是1；当m=_____时，函数的最小值是－2.5.如图，在同一坐标系中，函数y=ax+b与y=ax2+bx(ab≠0)的图象只可能是（）xyoABxyoCxyoDxyo6.二次函数y=ax2+bx+c的图象如图所示，下列各式中是正数的有（）①a②bc③④a+b+ca-b+c⑤⑥4a+b2a+b⑦By-1...12xyA.5个B.4个C.3个D.2个7.已知抛物线y＝ax2＋bx＋c的图象如图所示，下列结论：①a+b+c<0②a-b+c>0③acb>0④b=2a,其中正确的结论的个数是（）A.4B.3C.2D.110yx1-心理学家发现，学生对概念的接受能力y与提出概念所用的时间x(分钟)之间满足函数关系：y=－0.1x2+...