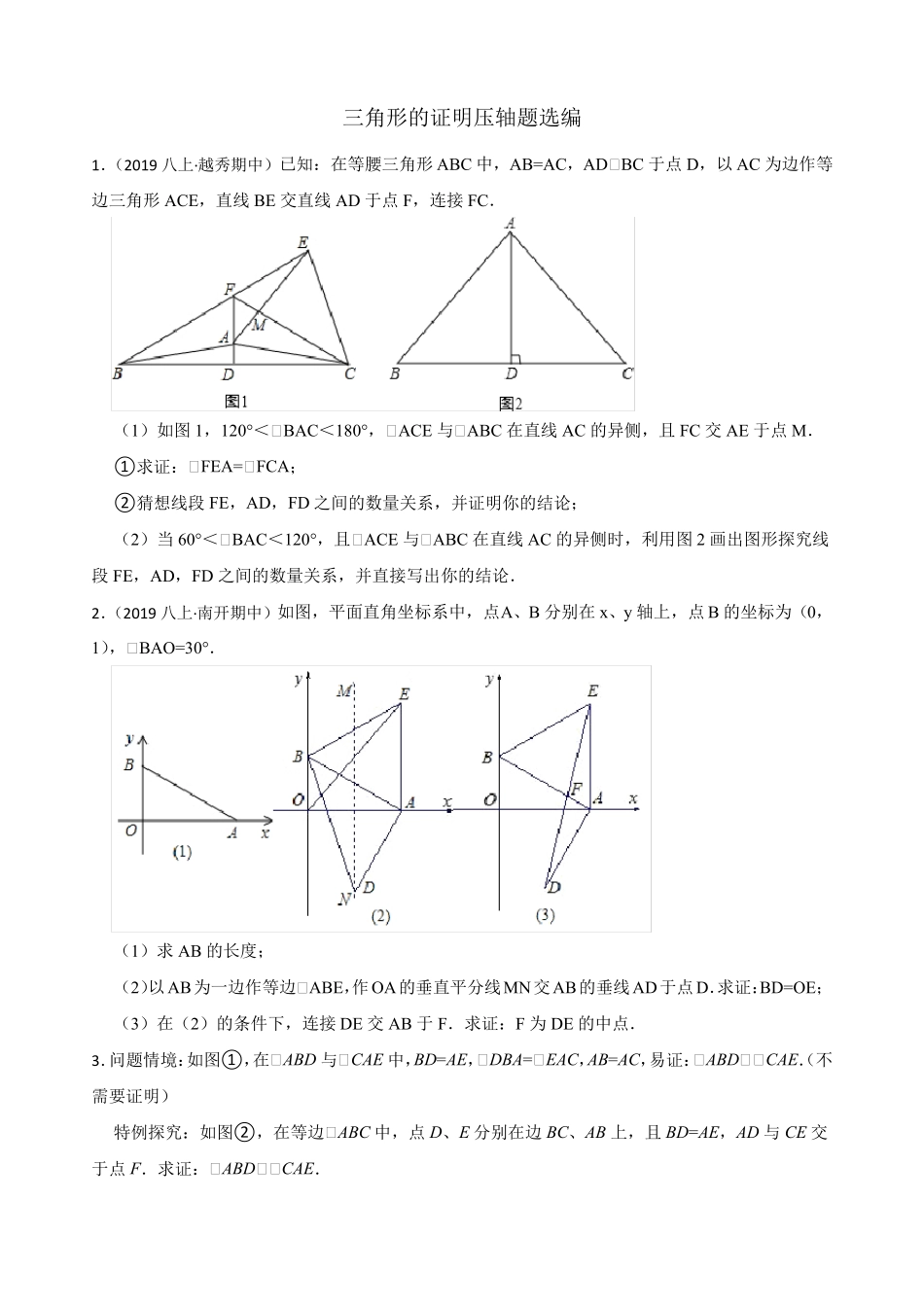
三角形的证明压轴题选编1.(2019八上·越秀期中)已知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.(1)如图1,120°<⊥BAC<180°,⊥ACE与⊥ABC在直线AC的异侧,且FC交AE于点M.①求证:⊥FEA=⊥FCA;②猜想线段FE,AD,FD之间的数量关系,并证明你的结论;(2)当60°<⊥BAC<120°,且⊥ACE与⊥ABC在直线AC的异侧时,利用图2画出图形探究线段FE,AD,FD之间的数量关系,并直接写出你的结论.2.(2019八上·南开期中)如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),⊥BAO=30°.(1)求AB的长度;(2)以AB为一边作等边⊥ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.3.BD=AE,⊥DBA=⊥EAC,AB=AC,⊥ABD⊥⊥CAE.问题情境:如图①,在⊥ABD与⊥CAE中,易证:(不需要证明)特例探究:如图②,在等边⊥ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:⊥ABD⊥⊥CAE.归纳证明:如图③,在等边⊥ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.⊥ABD与⊥CAE是否全等?如果全等,请证明;如果不全等,请说明理由.拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,⊥BAC=50°,⊥AEC=32°,求⊥BAD的度数.4.如图,已知在⊥ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后⊥BPD与⊥CQP是否全等,并说明理由;(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有⊥BPD与⊥CQP全等?(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿⊥ABC的三边上运动,经过多少时间点P与点Q第一次在⊥ABC的哪条边上相遇?5.(2021八上·灌云月考)如图,在⊥ABC中,AB=AC=4,⊥B=⊥C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作⊥ADE=50°,DE交线段AC于E.⊥EDC;⊥BDA逐渐变(填“大”(1)当⊥BDA=120°时,点D从B向C运动时,或“小”);(2)当DC等于多少时,⊥ABD⊥⊥DCE,请说明理由;(3)在点D的运动过程中,⊥ADE的形状可以是等腰三角形吗?若可以,请直接写出⊥BDA的度数,若不可以,请说明理由.6.(2021八上·温州月考)如图,在Rt⊥ABC中,⊥B=90°,AC=10,⊥C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.(1)DF=;(用含t的代数式表示)(2)求证:⊥AED⊥⊥FDE;(3)当t为何值时,⊥DEF是等边三角形?说明理由;(4)当t为何值时,⊥DEF为直角三角形?(请直接写出t的值.)7.(2021七下·新都期末)在等边⊥ABC中,点D是直线BC上的一个点(不与点B、C重合),以AD为边在AD右侧作等边⊥ADE,连接CE.(1)如图1,当点D在线段BC上时,求证:BD=CE;(2)如图2,当点D在线段BC的反向延长线上时,若⊥BAE=α,求⊥DEC的度数;(用含α的代数式表示)(3)如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S⊥ABC=4,求⊥ACF的面积.8.(2020八上·章贡期末)已知,如图AD为⊥ABC的中线,分别以AB和AC为一边在⊥ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,连接EF,⊥EAF+⊥BAC=180°(1)如图1,若⊥ABE=63°,⊥BAC=45°,求⊥FAC的度数;(2)如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;(3)如图2,设EF交AB于点G,交AC于点R,延长FC,EB交于点M,若点G为线段EF的中点,且⊥BAE=70°,请探究⊥ACB和⊥CAF的数量关系,并证明你的结论.9.()如图所示,⊥ABC是边长为6的等边三角形,P是AC边上一动点,由点A向点C运动(与A,C不重合),Q是CB延长线上的一点,与点...