二次函数图像与性质（2）VIP免费

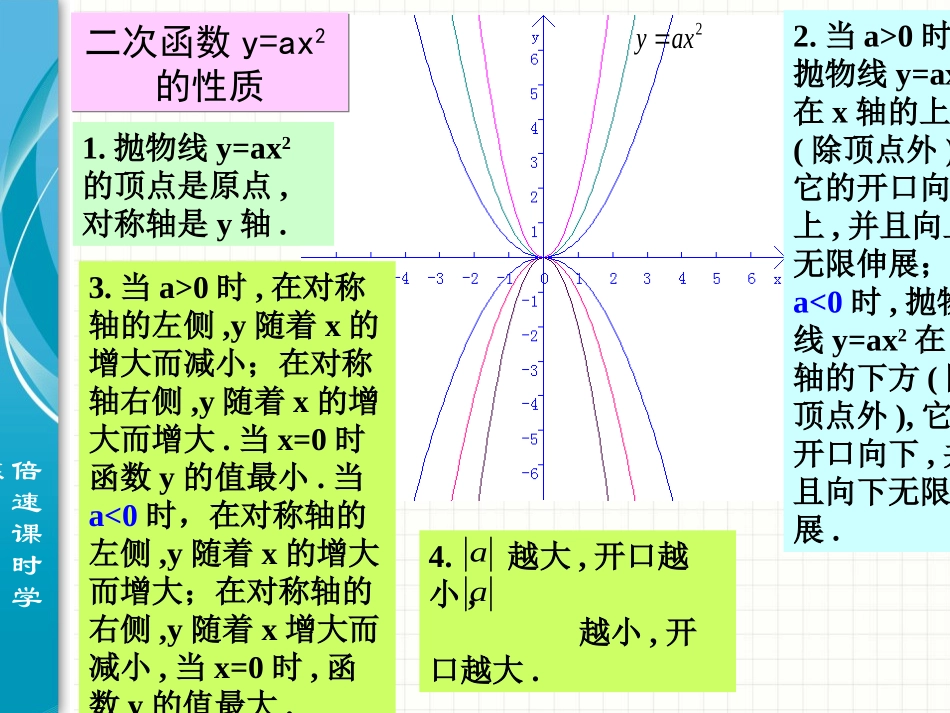
倍速课时学练北师大版九年级（下）2二次函数的图象与性质（2）倍速课时学练1.抛物线y=ax2的顶点是原点,对称轴是y轴.3.当a>0时,在对称轴的左侧,y随着x的增大而减小；在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.当a<0时，在对称轴的左侧,y随着x的增大而增大；在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质二次函数y=ax2的性质2axy2.当a>0时，抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展；当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.4.越大,开口越小,越小,开口越大.aa倍速课时学练二次函数y=ax2的性质１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值开口大小抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2(a>0)y=ax2(a<0)（0，0）（0，0）y轴y轴在x轴的上方(除顶点外)在x轴的下方(除顶点外)向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.根据图形填表：越小,开口越大.越大,开口越小.aa2axy倍速课时学练我思，我进步在同一坐标系中作出二次函数y=2x²+1的图象与二次函数y=2x²的图象.议一义二次函数y=2x²+1的图象与二次函数y=2x²的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?作图看一看．倍速课时学练122xy二次项系数为2,开口向上;开口大小相同;对称轴都是y轴;增减性与也相同.顶点不同,分别是原点(0,0)和(0,1).二次函数y=2x2+1的图象形状与y=2x2一样,仍是抛物线.二次函数y=2x2+1的图象是什么形状?它与二次函数y=2x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?22xy位置不同;最小值不同:分别是1和0.想一想,在同一坐标系中作二次函数y=-2x2+1和y=-2x2的图象,会是什么样?倍速课时学练y122xy二次项系数为-2,开口向下;开口大小相同;对称轴都是y轴;增减性与也相同.顶点不同,分别是原点(0,0)和(0,1).二次函数y=-2x2+1的图象形状与y=-2x2一样,仍是抛物线.二次函数y=-2x2+1的图象是什么形状?它与二次函数y=-2x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?22xy位置不同;最大值不同:分别是1和0..想一想,二次函数y=ax2+c和y=ax2的图象和性质?倍速课时学练x-2-1012y=2x2y=2x2+1y=2x2-182028yx2648024-2-4-271-11793139倍速课时学练我思，我进步在同一坐标系中作出二次函数y=3x²-1的图象与二次函数y=3x²的图象.议一义二次函数y=3x²一l的图象与二次函数y=3x²的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?倍速课时学练二次项系数为正数3,开口向上;开口大小相同;对称轴都是y轴;增减性与也相同.顶点不同,分别是原点(0,0)和(0,-1).二次函数y=3x2+1的图象形状与y=3x2一样,仍是抛物线.二次函数y=3x2-1的图象是什么形状?它与二次函数y=3x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?23xy位置不同;最大值不同:分别是1和0.132xy想一想,在同一坐标系中作二次函数y=-3x2-1和y=-3x2的图象,会是什么样?倍速课时学练二次项系数为正数-3,开口向下;开口大小相同;对称轴都是y轴;增减性与也相同.顶点不同,分别是原点(0,0)和(0,-1).二次函数y=3x2+1的图象形状与y=3x2一样,仍是抛物线.二次函数y=-3x2-1的图象是什么形状?它与二次函数y=-3x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?23xy位置不同;最大值不同:分别是0和-1.132xy请你总结二次函数y=ax2+c的图象和性质.倍速课时学练二次函数y=ax2+c的图象和性质１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+c(a>0)y=ax2+c(a<0)（0，c）（0，c）y轴y轴当c>0时,在x轴的上方(经过一,二象限);当c<0时,与x轴相交(经过一,二三四象限).当c<0时,在x轴的下方(经过三,四象限);当c>0时,与x轴相交(经过一,二三四象限).向上向下当x=...