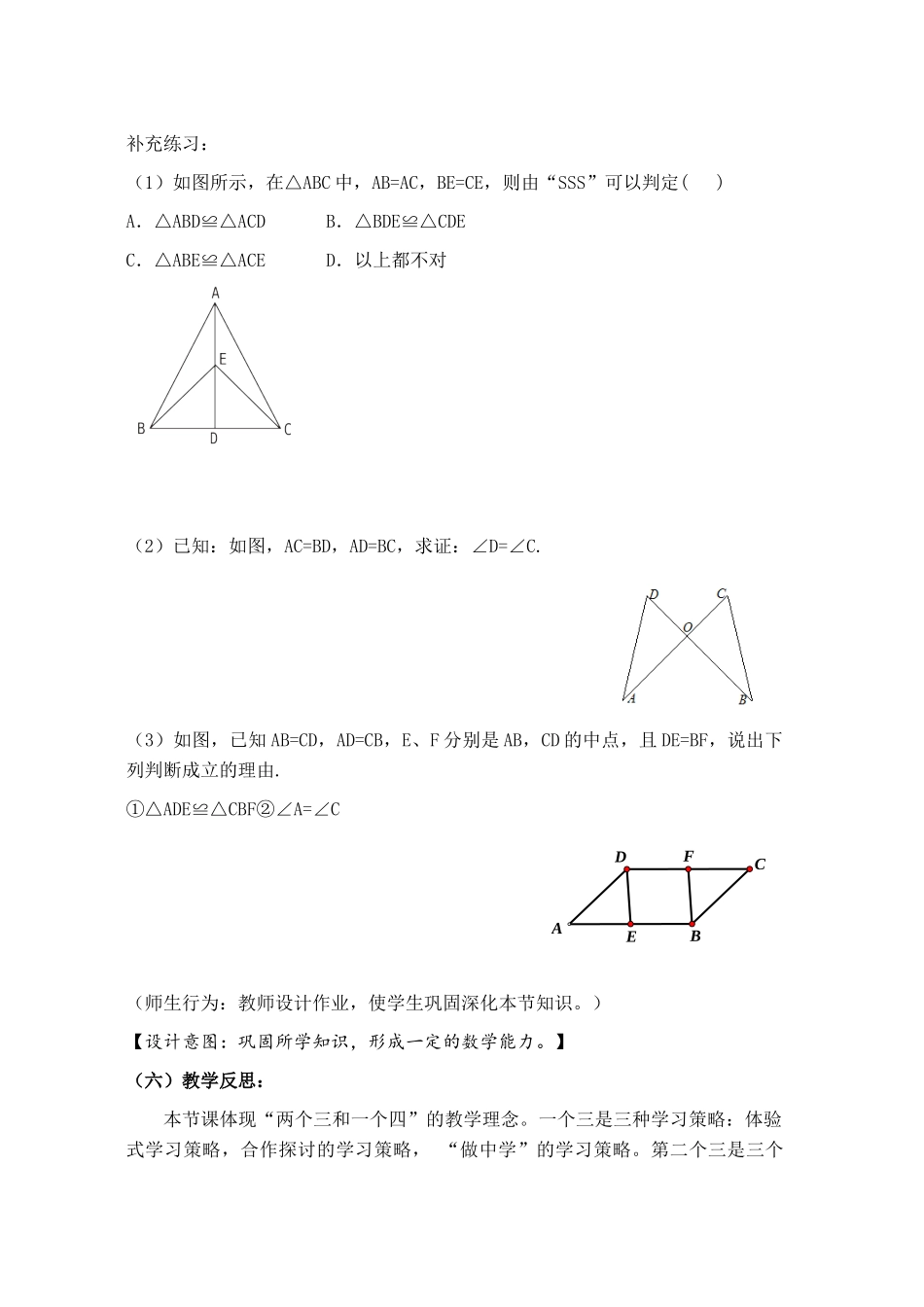
补充练习:(1)如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定()A.△ABD≌△ACDB.△BDE≌△CDEC.△ABE≌△ACED.以上都不对(2)已知:如图,AC=BD,AD=BC,求证:∠D=∠C.(3)如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C(师生行为:教师设计作业,使学生巩固深化本节知识。)【设计意图:巩固所学知识,形成一定的数学能力。】(六)教学反思:本节课体现“两个三和一个四”的教学理念。一个三是三种学习策略:体验式学习策略,合作探讨的学习策略,“做中学”的学习策略。第二个三是三个FEADBC解放:解放学生的大脑让学生多想,解放学生的嘴让学生多说,解放学生的手让学生多做。四是四种新观念:学习主题观,问题探究观,生命发展观,评价过程观。为实现教学目标,教学中,我将尽可能的让学生明白数学源自于生活,我们身边随处都有数学。课堂上,本着教师为引导,学生是主体的思想。而去引导学生观察,思考,讨论,动手实践等,从而得到新知。激发学生的兴趣也是教师教学中不能没有的教学理念,兴趣是学习的动力,是学习最好的导师。总之,最终的教学目标是,从教会学生数学,过渡到学生明白怎样会学数学。反思整个过程,我觉得做得较为成功的有以下几个方面:教学设计整体化,内容生活化。在课题的引入方面,然学生动手做、裁剪三角形。既提问复习了全等三角形的定义,又很好的过度到确定一个三角形需要哪些条件的问题上来。把知识不知不觉地体现出来,学得自然新鲜。数学学习来源于生活实际,学生学得轻松有趣。把课堂充分地让给了学生。我和学生做了些课前交流,临上课前我先对他们提了四个要求:认真听讲,积极思考,大胆尝试,踊跃发言。其实,这是一个调动学生积极性,同时也是激励彼此的过程。在上课过程中,我尽量不做过多的讲解,通过引导让学生发现问题并通过动手操作、交流讨论来解决问题。在难点的突破上取得了成功。