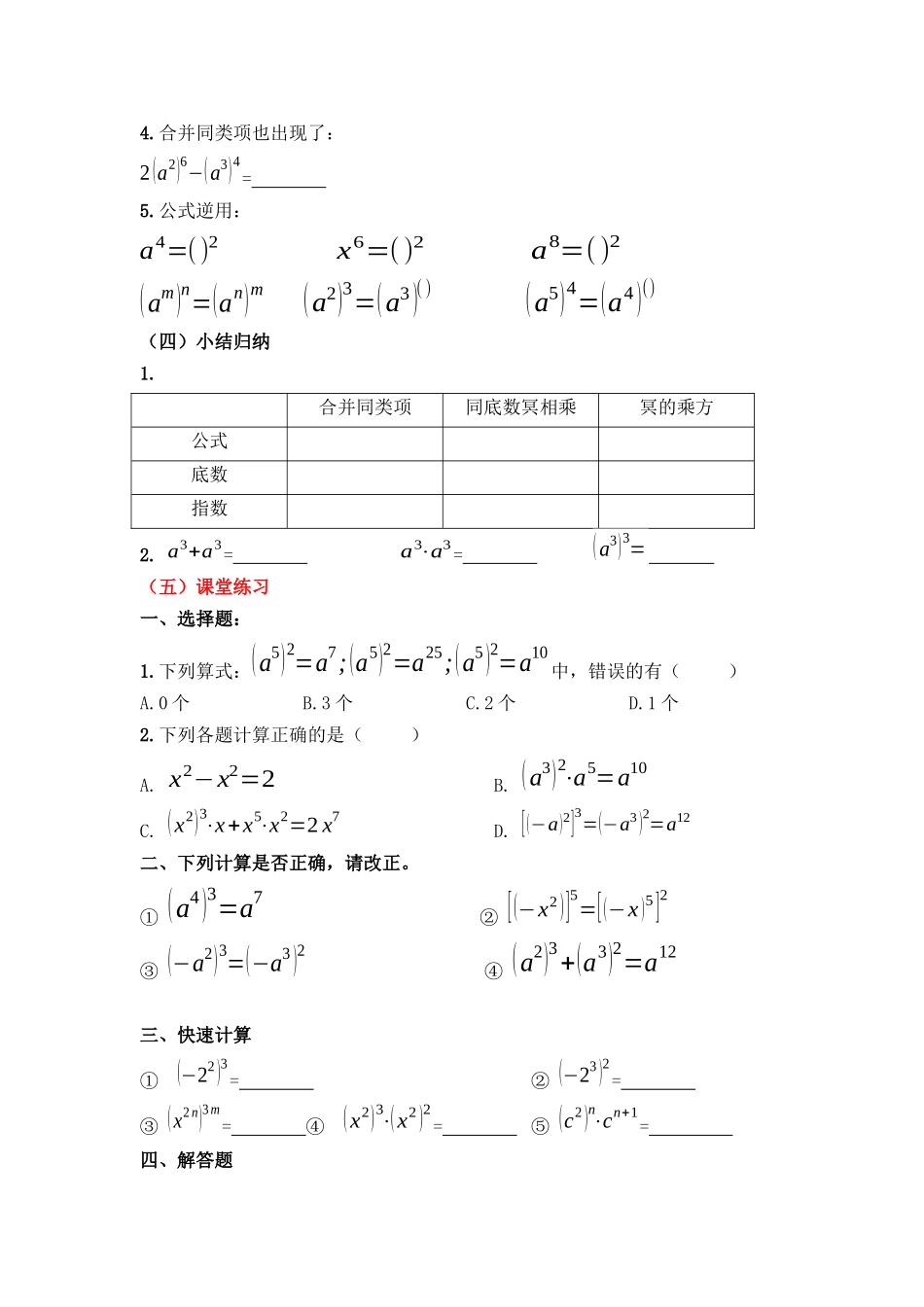
14.1.2幂的乘方教学案【学习目标】1.能理解幂的乘方的意义,并能用符号语言准确描述.2.经历探索幂的乘方的运算法则过程,理解幂的乘方的运算法则,并进一步发展推理及归纳能力.3.会区分同底数的乘法、幂的乘方等运算。【学习重点】理解并正确运用幂的乘方及运算.【学习难点】幂的乘方的探究过程及应用.【学习过程】(一)学前准备:复习旧知幂1.计算①(−a)2⋅(−a)3⋅(−a)②(−x)⋅x2⋅(−x)4③xm⋅xm+1⋅x④(x+y)2⋅(x+y)n−22.(1)已知3n⋅3n+1=313,求n的值3.(1)已知2a=4,2b=5,求2a+b的值;(2)已知2a=4,2b=5,求2a+b+3的值4.乘方的意义103=10××an·an·an=数数an(102)3=××(乘方的意义)=10(2+2+2)(同底数幂的乘法)=10(2×3)(二)回归教材、解读教材:1.理解幂的乘方的含义(am)n→再求n次乘方运算底数是一个幂推广为:(an)2=¿(an)3=¿¿=a(n+n)=a(n+n+n)=a()=a()2.证明过程:(am)n===amn(m,n都是正整数)3.你能用语言描述这一法则吗?(文字语言)幂的乘方法则:=.(三)学以致用:1.(1)(102)3=(2)(b5)5=(3)(an)3=(4)[(−2)3]2=(5)[(a+b)2]4=(6)(x2n)2=深度挖掘教材:2.负号捣乱来了:[(−2)3]3=[(−p)4]3=—(xm)n=3.同底数幂相乘也出现了:(y2)3⋅y=(x3)3⋅(y2)2=↓4.合并同类项也出现了:2(a2)6−(a3)4=5.公式逆用:a4=()2x6=()2a8=()2(am)n=(an)m(a2)3=(a3)()(a5)4=(a4)()(四)小结归纳1.合并同类项同底数冥相乘冥的乘方公式底数指数2.a3+a3=a3⋅a3=(a3)3=(五)课堂练习一、选择题:1.下列算式:(a5)2=a7;(a5)2=a25;(a5)2=a10中,错误的有()A.0个B.3个C.2个D.1个2.下列各题计算正确的是()A.x2−x2=2B.(a3)2⋅a5=a10C.(x2)3⋅x+x5⋅x2=2x7D.[(−a)2]3=(−a3)2=a12二、下列计算是否正确,请改正。①(a4)3=a7②[(−x2)]5=[(−x)5]2③(−a2)3=(−a3)2④(a2)3+(a3)2=a12三、快速计算①(−22)3=②(−23)2=③(x2n)3m=④(x2)3⋅(x2)2=⑤(c2)n⋅cn+1=四、解答题1.(1)已知求的值;(2)已知,求的值.2.已知,,试比较a,b,c的大小.3.当n为奇数时,________.