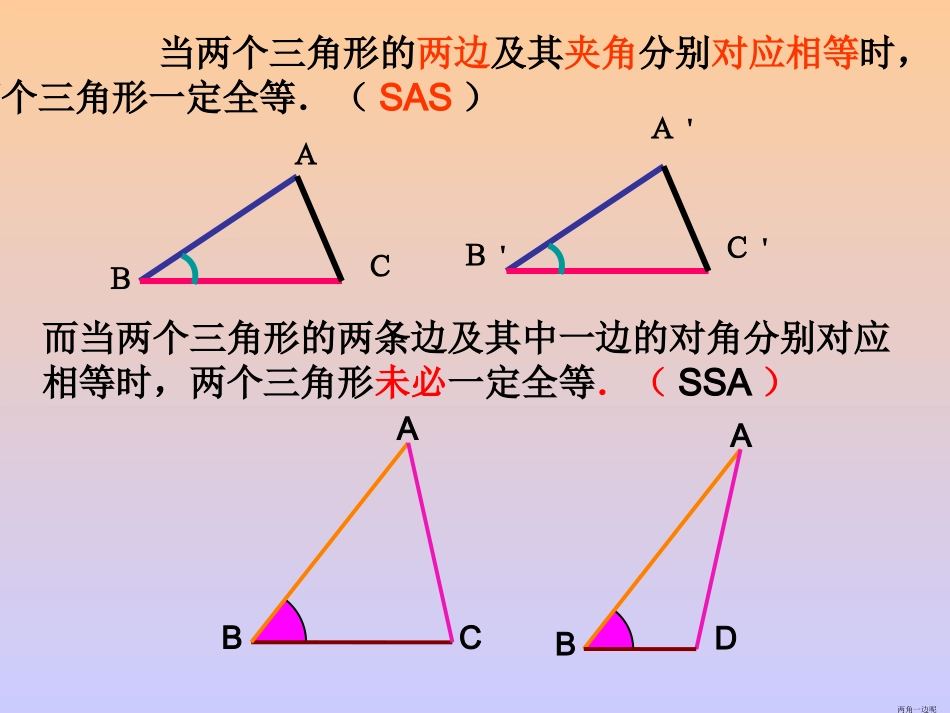
12.2.312.2.3全等三角形的判定(三)全等三角形的判定(三)回顾:(1)给定三角形的一个条件:可能出现的结果是:一条边一个角(2)给定三角形的两个条件时:可能出现的结果是:两条边两个角一边一角(3)给定三个条件时:可能出现的结果是:三个角三条边两边对一角两角一边两边夹一角当两个三角形的两边及其夹角分别对应相等时,两个三角形一定全等.(SAS)而当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形未必一定全等.(SSA)两角一边呢BA'B'C'ACABDABC已知:如图,要得到△ABCABD,≌△已经隐含有条件是_________根据所给的判定方法,在下列横线上写出还需要的两个条件(1)(SAS)(2)(SAS)ABCDAB=ABAC=AD∠CAB=DAB∠BC=BD∠CBA=DBA∠教学目的:1、会说出三角形全等判定的角边角公理及其推论(角角边);2、会应用角边角公理和角角边定理证明两个三角形全等,进而证明线段(全等三角形对应边)相等或角(全等三角形对应角)相等。3、在帮助学生熟悉公理的应用中,进一步渗透综合法和分析法的思想方法,从而提高学生演绎推理的条理性和逻辑性。二、提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?①②③要不要要不要33块都带去?块都带去?带几块,带去了三角形的几个元素?带几块,带去了三角形的几个元素?另外两块呢?另外两块呢?三、合作学习:有两个角和这两个角的夹边对应相等的两个三角形一定全等吗?请用量角器和刻度尺画ΔABC,使BC=3,∠B=400、∠C=600将你画的三角形与其他同学画的三角形比较,你发现了什么?CBA6004003cm有两个角和这两个角的夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”)剪下来,与同伴进行比较,它们能否互相重合?已知:任意△ABC,画一个△A’B’C’,使A’B’=AB,∠A’=A∠,∠B’=B∠问:通过实验可以发现什么事实?画法:1、画A’B’=AB2、在A’B’的同旁画∠DA’B’=A∠,∠EB’A’=B∠,A’D、B’E交于点C’。∴△A’B’C’就是所要画的三角形。A'B’C’ABCDE有两角和它们夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”)如果两个三角形的两角及其夹边分别对应相等,那么这两个三角形全等.归纳简记为(A.S.A.)或角边角CBAFED符号语言ABCDEFB=E(BC=EF(C=F(ABCDEFA.S.A.在和中已知)已知)已知)()≌三角形全等的识别B’C’A'ABC(ASA)________()________()________()证明:在和中∴△____________≌△∠A=A’∠已知AB=A’B’已知∠B=B’∠已知ABCA’B’C’△ABCA’B’C’△已知:如图,AB=A’B’,∠A=A’∠,∠B=B’∠。求证:△ABC≌A’B’C’△1、某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()。A带①去B带②去C带③去D带①和②去①②③c2、如图,AC与BD相交于点O,则:1.图中可看出相等的是______=______.2.要证△BAODOC≌△还需要_____个条件.3.请补充条件,填写证明方案._______________________________________根据:______________________________________________根据:______________________________________________根据:_______ABDCO∠AOB∠COD2OA=OC∠AOB=COD∠OB=ODSAS∠AOB=COD∠OB=OD∠B=D∠ASA∠AOB=COD∠OA=OC∠A=C∠ASA**如图19.2.9,已知∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABCDCB△.图19.2.93∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,证明在△ABC和△DCB中, ∴△ABCDCB≌△()A.S.A.AAS?如果两个三角形有两个角及其中一角的对边分别对应相等,那么这两个三角形能全等吗?〖探究方法〗——用逻辑推理方法证明如图:如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?已知:∠A=∠A′,∠B=∠B′,AC=A′C′求证:△ABCA′B′C′≌△证明 ∠A=∠A′,∠B=∠B′又∠A+∠B+∠C=180°(三角形的内角和等于180°)同理∠A′+∠B′+∠C′=180°∴∠C=∠C′.在△ABC和△A′B′C′中 ∠A=∠A′AC=A′C′...