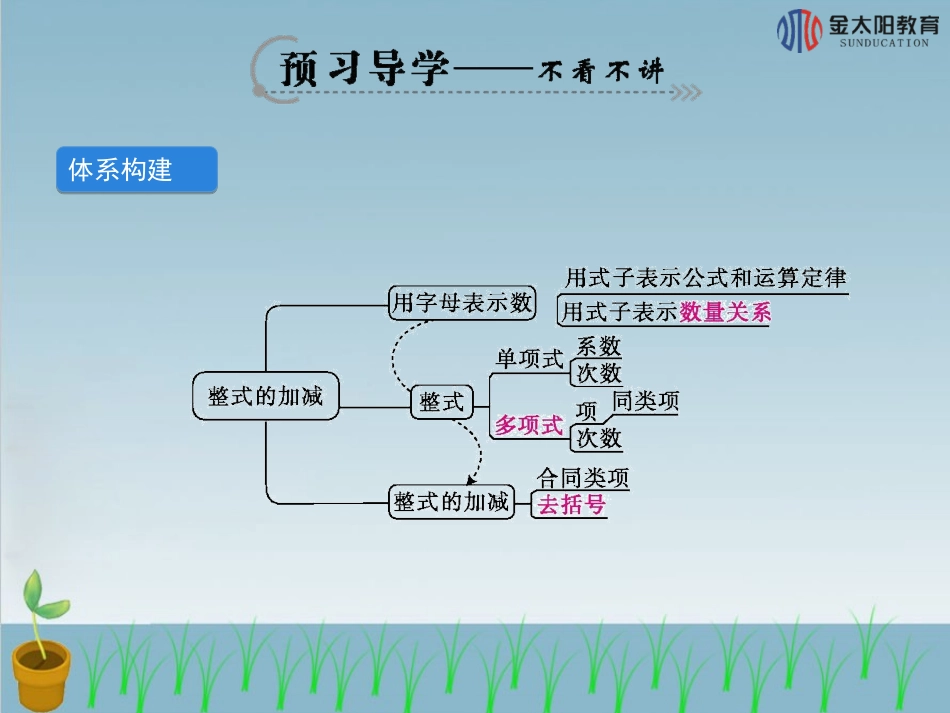
第二章复习课第二章复习课1.知道单项式、多项式及其相关概念,能用整式表示实际问题中的数量关系.2.认识同类项,并能合并同类项.3.熟记去括号法则,并能利用去括号法则正确地去括号.4.能利用整式加减的运算法则进行相关计算和化简.5.重点:同类项以及合并同类项,去括号法则,以及整式加减运算的法则.体系构建核心梳理数字母单项式数字因数所有字母指数的和最高次项的次数不含有字母的项多项式里的每个单项式1.单项式:与的积叫作单项式,单独的一个数或字母也是单项式.①单项式中的叫作这个单项式的系数.②一个单项式中,叫作这个单项式的次数.2.多项式:几个的和,叫作多项式.①叫作多项式的项,叫作常数项.②多项式中叫作多项式的次数.3.同类项:相同,并且也相同的项叫作同类项.(1)同类项:把多项式中的同类项,叫作合并同类项.(2)合并同类项的法则是:①,②.4.去括号法则:①如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号;②如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号.5.整式的加减的一般步骤:①如果有括号,应先;②去括号后,如果有同类项,再.相同字母的指数所含字母合并成一项同类项的系数相加减,所得结果作为系数字母和字母的指数不变相同相反去括号合并同类项3a-5专题一:用字母表示数1.某工厂一月份加工产品a件,二月份加工的产品数比一月份加工的产品数的3倍少5件,则二月份加工产品件.2.一个两位数,个位数字为x,十位数字为y,则这个两位数是.10y+x[变式训练1]x表示一个两位数,把3写到x的右边组成一个三位数,则表示这个三位数的代数式是()A.3xB.10x+3C.100x+3D.3×100+x[变式训练2]x表示一个两位数,把3写到x的左边组成一个三位数,则表示这个三位数的代数式是()A.3xB.10x+3C.100x+3D.3×100+xBD3.如图是用相同长度的小棒摆成的一组有规律的图案,图案(1)需要4根小棒,图案(2)需要10根小棒……按此规律摆下去,第n个图案需要小棒根(用含有n的代数式表示)4.按下图方式摆放餐桌和椅子.6n-2(1)1张餐桌可坐人;2张餐桌可坐人.(2)按照上图的方式继续排列餐桌,完成下表:桌子张数3456…n可坐人数61014182226…4n+2[变式训练]按下图方式摆放餐桌和椅子:(1)若按照上图的摆法摆放餐桌和椅子,完成下表:桌子张数1234…n可坐人数681012…2n+4(2)一家餐厅有40张这样的长方形桌子,按照上图方式,每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐人.【方法归纳交流】如何探索和表达出规律呢?可从以下三个层次来突破:一是寻找数量关系;二是用式子表示出规律;三是规律.112验证专题二:整式的有关概念15.在代数式0,a2+1,x2y,(a+b)(a-b),1m+1,-a,x2-2xy+1,-23a2b中,单项式有;多项式有,整式有.0,x2y,-a,-𝟐𝟑a2ba2+1,(a+b)(a-b),x2-2xy+10,x2y,-a,-𝟐𝟑a2b,a2+1,(a+b)(a-b),x2-2xy+16.-2πh5的系数是,次数是.-𝟐𝛑𝟓[变式训练]如果关于x的多项式mx4+4x2-12与3xn+5x的次数相同,求12n3-2n2+3n-4的值.(教师可通过此题让学生体会分类讨论的数学思想)解:由题意,(1)当m=0时,n=2,𝟏𝟐n3-2n2+3n-4=𝟏𝟐×23-2×22+3×2-4=-2;(2)当m≠0时,n=4,𝟏𝟐n3-2n2+3n-4=𝟏𝟐×43-2×42+3×4-4=32-32+12-4=8.【方法归纳交流】多项式的次数相等意味着两个或更多个多项式的的次数相等.7.多项式x2y―2xy+3是三次三项式,二次项的系数是.专题三:同类项的概念8.下列各组式子中,是同类项的是()A.3x2y与-3xy2B.3xy与-2yxC.2x与2x2D.5xy与5yz9.写出-2x2y的三个同类项:.最高次项-2Bx2y,-x2y,2x2y(答案不唯一)10.若-2xmyn+2与3x2y6是同类项,则(-m)n=.[变式训练]若同类项mx2a+2y2与0.4xy3b+4的和为0,求m和a,b的值.【方法归纳交流】从同类项的定义可以知道,一个单项式的同类项有个,它们的共同特征是含有的字母相同,相同字母的相同,与字母的先后顺序.16无数指数无关解:由题意,得mx2a+2y2与0.4xy3b+4是同类项,且m=-0.4,于是,2a+2=1,3b+4=2,所以a=-𝟏𝟐,b=-𝟐𝟑.专题四:去括号法则11.去括号:a-2(b-c)=a-;添括号:a-b-c=a-.12.下列各题去括号所得结果正确的是()A.x2-(x-y+2z)=x2-x+y+2zB.x-2(-2x+3y-1)=x+4x-6y+1C.3x-[5x-(x-1)]=3x-5x-x+1D.(x-1)-2(x2-2)=x-1-2x2+4【方法归纳交流】当多项式中含有大、中、小括号时,通...