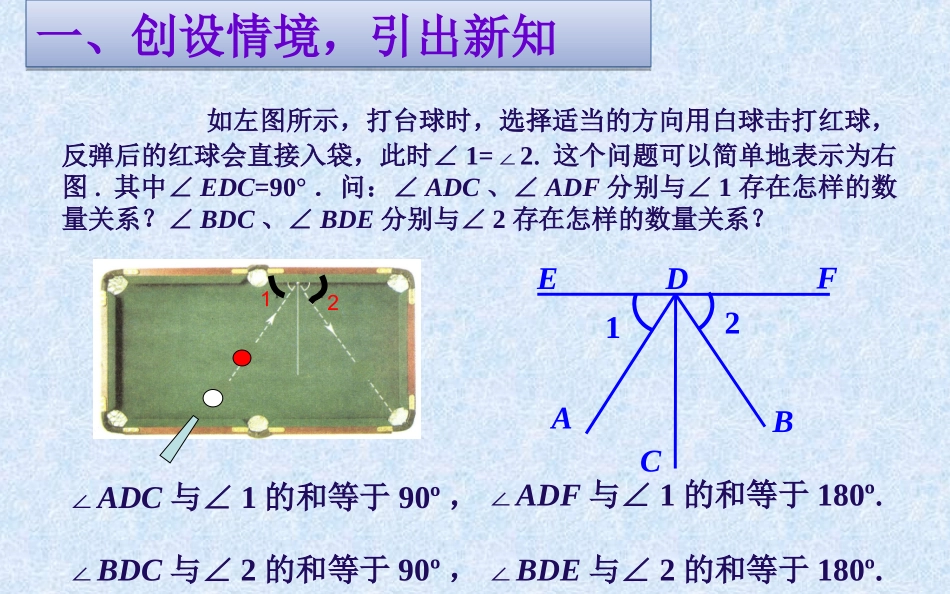
太行路学校赵琳一、创设情境,引出新知一、创设情境,引出新知如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90°.问:∠ADC、∠ADF分别与∠1存在怎样的数量关系?∠BDC、∠BDE分别与∠2存在怎样的数量关系?12ACBEDF12∠ADC与∠1的和等于90º,∠ADF与∠1的和等于180º.∠BDC与∠2的和等于90º,∠BDE与∠2的和等于180º.二、新知探究:1、如果两个角的和等于900(直角),那么就说这两个角互为余角,其中每一个角是另一个角的余角.1、如果两个角的和等于900(直角),那么就说这两个角互为余角,其中每一个角是另一个角的余角.如图1:说明:互余两个角可以不都是锐角,如0°与90°的两个角也是互余。二、新知探究:2、如果两个角的和为1800(平角),就说这两个角互为补角,其中每一个角是另一个角的补角.二、新知探究:2、如果两个角的和为1800(平角),就说这两个角互为补角,其中每一个角是另一个角的补角。如图2:二、新知探究:2、如果两个角的和为1800(平角),就说这两个角互为补角,其中每一个角是另一个角的补角。如图3:二、新知探究:1.定义中的“互为”是什么意思?2.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?三、理解定义,巩固运用三、理解定义,巩固运用1ADF11即每一个角都是另一个角的余角(补角)互为补角(余角)的两个角与位置无关。四、学以致用:(1)420角与480角互为余角()(2)280角与720角互为余角()(3)∠5+∠6+∠7=900,则∠5、∠6、∠7互为余角()(4)两个锐角一定互为余角.()(5)两个直角互为补角。()(6)72°角的补角是128°()(7)一个锐角与一个钝角一定互为补角.()1、判断正误互为余角只是对两个角而言的。图中给出的各角,哪些互为余角?10o30o60o80o50o40o2、连连看:图中给出的各角,那些互为补角?30o60o80o100o120o150o试一试:∠α∠α的余角∠α的补角5°32°62°23′70°39′X85°175°58°148°117°37′180°°-∠∠109°21′27°37′∠∠(∠∠<90°)的余角是。∠∠的补角是。则一个角的补角比它的余角大。90°°--∠∠90°90°归纳:归纳:90°°-X180°°-X19°21′例1、若∠A+27°=90°B+27°=90°∠则∠A与∠B的关系∵∠A+27°=90°∠B+27°=90°∴∠A=90°-27°=63°∠B=90°-27°=63°∴∠A=B∠相等结论:同角(或等角)的余角相等五、例题解析理由:例2、若∠5+100°=180°6+100°=180°∠则∠5与∠6的关系是相等理由:∵∠5+100°=180°∠6+100°=180°∴∠5=6∠结论:同角(或等角)的补角相等五、例题解析六、互为余角与互为补角的性质1、同角(或等角)的余角相等2、同角(或等角)的补角相等已知一个角的补角是它的余角的4倍,求这个角的度数。解:设这个角为x度,则它的余角是度,它的补角是度.(90-x)(180-x)依题意得180-x=4(90-x)即:这个角的度数为60º七、范例讲解180-x=360-4x-x+4x=360-1803x=180x=60学以致用:1、一个角的余角是它补角的三分之一,则这个角是多少度?八、思考题:41、如图:图中互为余角有对,分别是ACBD∠A与∠B、∠ACD与∠A∠ACD与∠BCD、∠BCD与∠B图中有相等的角吗?若有,请写出来,并说明理由2、如图:ACBD理由:∵△ABC的内角和为180°∠ACB=90°∴∠A+B=180°∠-90°=90°∴∠A是∠B的余角同理∠DCB是∠B的余角∴∠A=DCB∠(同角的余角相等)同理:∠B=ACD∠答:有相等的角,分别是∠A=DCB∠,∠B=ACD∠,∠ACB=ADC=CDB∠∠1、谈谈你这节课的收获。九、小结:2、这节课你的表现怎么评价。