1.3不共线三点确定二次函数的表达式VIP免费

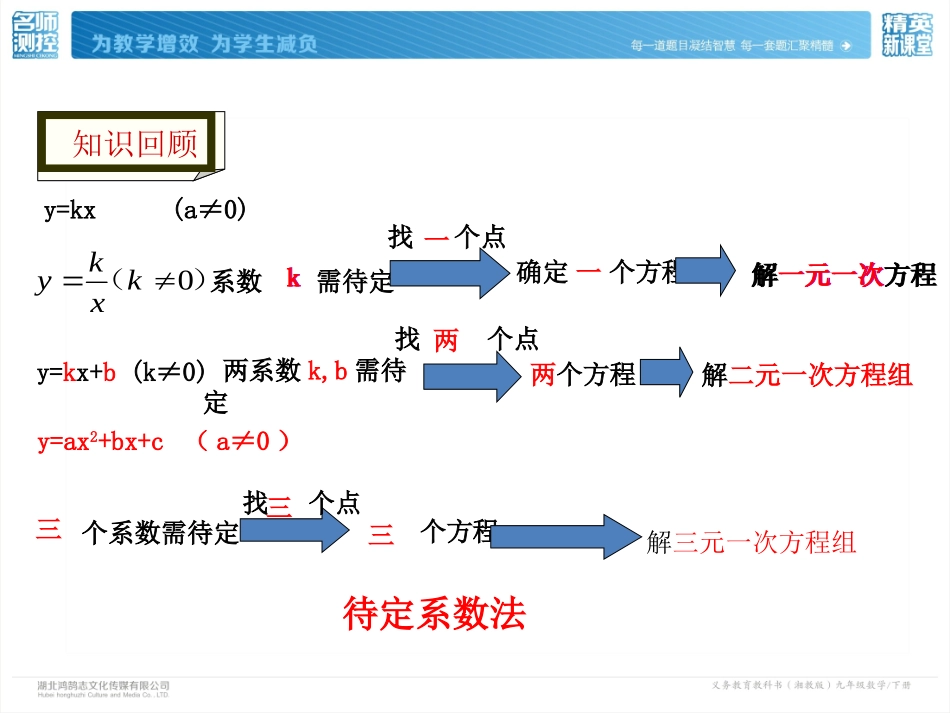
第1章二次函数1.3不共线的三点确定二次函数的表达式y=kx(a≠0)y=kx+b(k≠0)系数需待定找个点确定个方程解一元一次方程两系数k,b需待定找个点两个方程解二元一次方程组y=ax2+bx+c（a≠0）个系数需待定找个点个方程解三元一次方程组待定系数法）（0kxkyk一一两三三三知识回顾解一元一次方程k例1、已知一个二次函数的图象经过点（1，3），（-1，﹣5），（3，﹣13）。（1）求这个二次函数的解析式；（2）写出它的对称轴和顶点坐标。新知探究议一议小组讨论合作探究一般式的基本步骤？1.设2.找3.列4.解5.写6.查（三元一次方程组）（三点）（一般形式）y=ax2+bx+c（消元）（回代)选择合适的方法求二次函数解析式：1、抛物线经过（2，0）（0，-2）（-1，0）三点。2、抛物线的顶点坐标是（6，-2），且与X轴的一个交点的横坐标是8。22yxx2211(6)261622yxxx随堂练习顶点式1.设y=a(x-h)2+k2.找（一点）3.列（一元一次方程）4.解（消元）5.写（一般形式）6.查（回代）一般式1.设y=ax2+bx+c2.找（三点）3.列（三元一次方程组）4.解（消元）5.写（一般形式）6.查（回代）区别巩固1、求二次函数解析式的常用方法：2、求二次函数解析式的常用思想：3、二次函数解析式的最终形式：一般式转化思想解方程或方程组无论采用哪一种表达式求解，最后结果都化为一般形式。顶点式数形结合思想二、求二次函数解析式的思想方法2、是否有函数经过三点.已知图象上三点坐标，通常选择一般式。.已知图象的顶点坐标（对称轴或最值），通常选择顶点式。确定二次函数的解析式的关键是根据条件的特点，恰当地选择一种函数表达式，灵活应用。1、求二次函数解析式的一般方法：