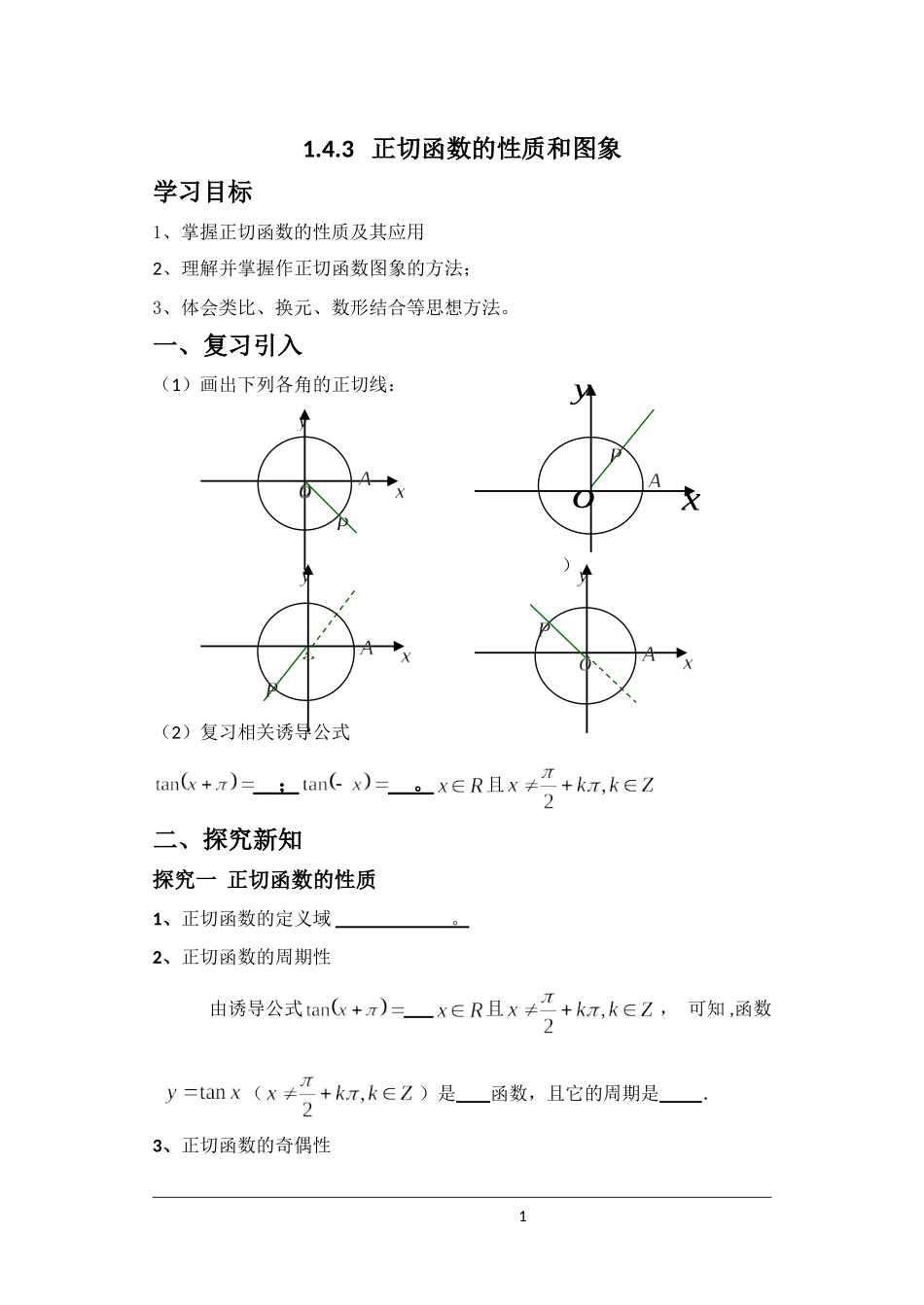
1.4.3正切函数的性质和图象学习目标1、掌握正切函数的性质及其应用2、理解并掌握作正切函数图象的方法;3、体会类比、换元、数形结合等思想方法。一、复习引入(1)画出下列各角的正切线:(2)复习相关诱导公式;。且二、探究新知探究一正切函数的性质1、正切函数的定义域。2、正切函数的周期性由诱导公式且,可知,函数()是函数,且它的周期是.3、正切函数的奇偶性1)xyo因为且,所以正切函数()是函数.4、正切函数的单调性由图(Ⅰ)、(Ⅱ)正切线的变化规律可以得出,正切函数在内是函数,又由正切函数的周期性可知,正切函数在开区间内都是增函数.5、正切函数的值域由图(Ⅰ)可知,当大于且无限接近于时,正切线向轴的负方向无限延伸;由图(Ⅱ)可知,当小于且无限接近于时,正切线向轴的正方向无限延伸.因此,在内可以取任意实数,但没有最大值、最小值.因此,正切函数的值域是.探究二正切函数的图像21.利用正切线画出,的图象:2.根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数,且的图象,称“正切曲线”.3、如何快速作出正切函数的简图?4、根据图像讨论验证正切函数的性质。三、新知运用例1求函数的定义域、周期和单调区间.111oxy0.3023223yx例2解不等式四、课堂练习1、求函数y=tan3x的定义域,值域,单调增区间。2、观察正切曲线,写出满足下列条件x的范围:(1);(2);(3)六、课后作业教材46页,习题1.4A组6,7,8,9.4