函数单调性讲课VIP免费

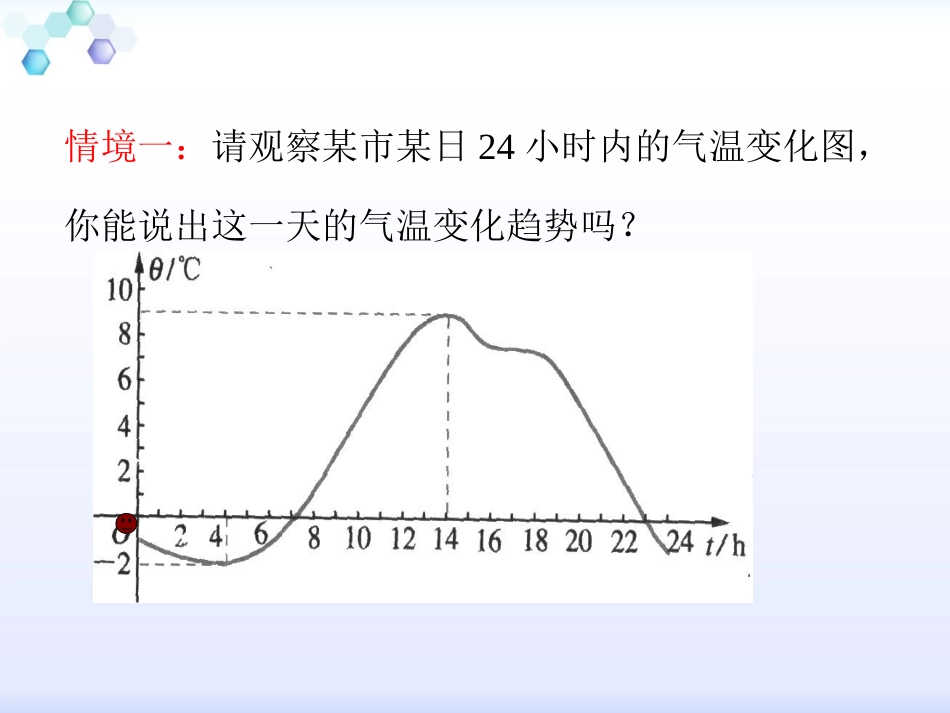
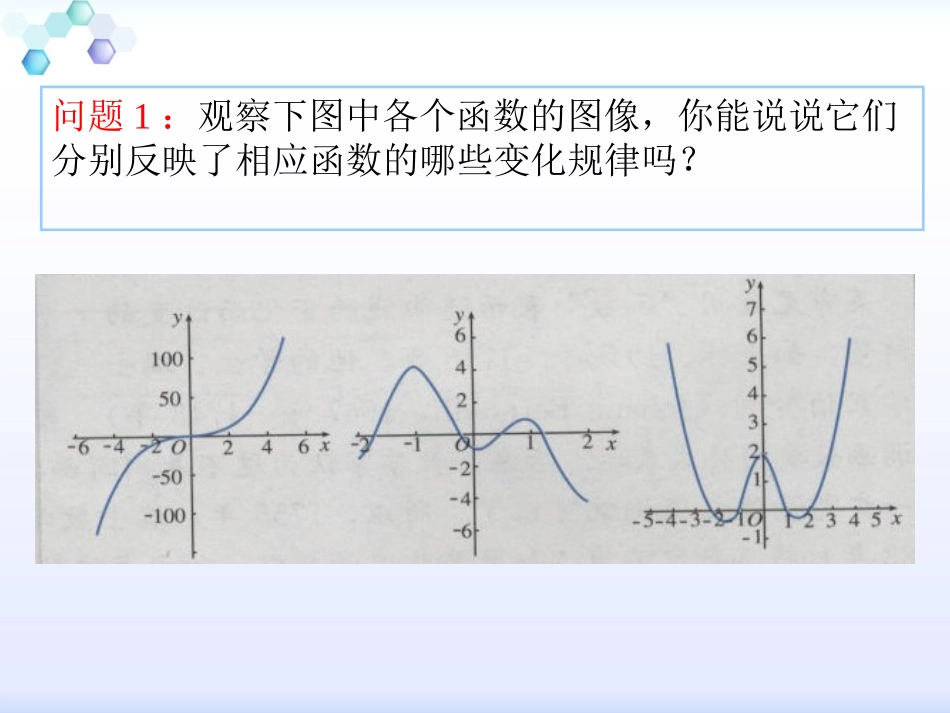
1.3.1函数的单调性【学习目标】1、理解增函数、减函数的概念及函数单调性的定义2、会根据函数的图像判断函数的单调性3、能根据单调性的定义证明函数在某一区间上是增函数还是减函数重点：函数单调性的定义及单调性判断和证明难点：函数单调性的判断和证明情境一：请观察某市某日24小时内的气温变化图，你能说出这一天的气温变化趋势吗？问题1：观察下图中各个函数的图像，你能说说它们分别反映了相应函数的哪些变化规律吗？xy–1–2–3123–1–2–3123O问题2观察函数fxx和2fxx图象，随着x增大图象是如何变化的？xy–1–2–312312345Oxy–1–2–312312345O初步认识函数单调性函数的定义域为：图象在y轴左侧随着x增大而：我们就说函数在上为减函数2fxx2fxxR下降0+，图象在y轴右侧随着x增大而：我们就说函数在上为增函数2fxx上升-0，xy–1–2–312312345O…-4-3-2-101234………x2()fxx16941410169问题3函数2fxx的图象在y轴右侧随着x的增大是上升的，如何用数学语言来描述这种“上升”呢？函数2fxx在区间0,上图象随x的增大而上升，在区间0,上y随x的增大而增大.问题4如何用数学符号语言描述函数2fxx在0+，y随x的增大而增大？xy–1–2–312312345O1fx2fx2x1x在区间上任意取的值，当时，都有0+，12,xx12xx我们就说函数在上为增函数2fxx2fxx0+，12()()fxfx设函数定义域为：()fxI如果对于属于定义域内IA变量的值，当时，都有，12,xx12xx12()()fxfx那么就说在这个区间上是增函数.()fx1x2x1)(fx2)(fx)(yfxxy某个区间任意上的两个自增函数的定义：问题5如何用数学符号语言描述函数2fxx在,0y随x的增大而减小？xy–1–2–312312345O1fx2fx2x1x函数2()fxx定义域为R:在,0上任意的12,xx的值，当12xx时，都有12()()fxfx．我们就说函数2()fxx在区间,0上减函数．设函数定义域为()fxI如果对于属于定义域内某个区间上的任意两个自IA变量的值，当时，都有，12,xx12xx12()()fxfx那么就说在这个区间上是减函数.()fx1x2x1)(fx2)(fx)(yfxxy减函数的定义:如果函数在某个区间是增函数或减函数，那么就说函数在这一区间具有（严格的）单调性.()fx()fx这一区间叫做函数的一个单调区间.()fx不同之处：在单调区间上，增函数的图象是上升的，减函数的图象是下降的.函数的单调性定义例1右图是定义在区间[5,5]上的函数的图像，根据()yfx图像说出的单调区间，以及在()yfx每一单调区间上，是增函数还是()yfx减函数．12345-5-4-3-2-1123-1-2xyo解:函数的单调区间有[-5，-2)，[-2，1)，[1，3)，[3，5]，其中函数在区间[-5，-2)，[1，3)上是减函数,在区间[-2，1)，[3，5]上是增函数.()fx()fx例2证明函数在上是增函数．()32fxxR证明：12,,xxR且12,xx任取1212()()(32)(32)fxfxxx123().xx由，得，12xx120xx于是120()()fxfx即12()(),fxfx所以，在上是增函数．()32fxxR取值作差变形定号判断物理学中的玻意耳定律(k为正常数)告诉我们,对于一定量的气体,当其体积减小时,压强p将增大,试用函数的单调性证明之。kpV则1212()()kkpVpVVV2112VVkVV12,0,VV，且12VV21120,0VVVV1212()()0,()()pVpVpVpV所以函数在区间上是减函数.,0,kpVV0,证明：设是在上任取的两个实数,且0,12VV12,VV又0k,于是取值作差变形定号结论练习本节课重点增函数与减函数的定义．增函数与减函数的的证明．本节课难点增函数与减函数的证明：图象法及定义法．书面题：P39第1、２、３题思考题：画出函数的图象并判断其在定义域上有怎样的单调性？预习题：预习教材P30至P32.1()fxx布置作业