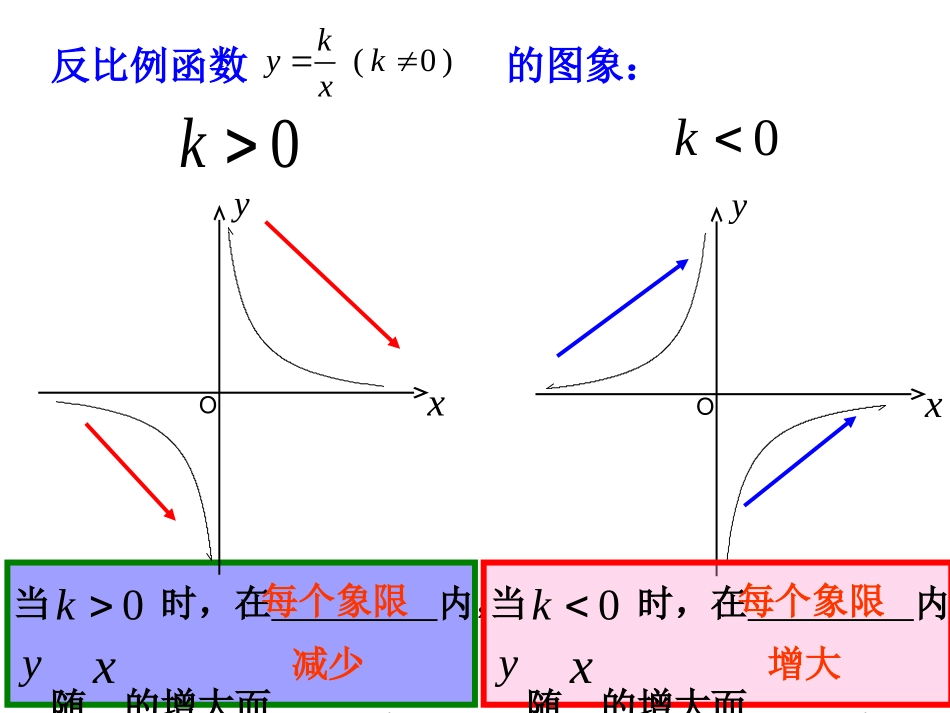
26.2实际问题与反比例函数(一)建工师二中李卫华九年级下册忆一忆忆一忆什么是反比例函数?反比例函数图象是什么?反比例函数的性质?当时,在内,随的增大而.yx0kxyO反比例函数的图象:(0)kykx0k0kxyO减少每个象限当时,在内,随的增大而.yx0k增大每个象限pV=k(k为常数,k>0)这是波义耳在1662年通过实验研究出的结果,公式通常称为波义耳定律.1、使劲踩气球时,气球为什么会爆炸?在温度不变的情况下,气球内气体的压强p(Pa)与它的体积V()的乘积是一个常数k.3m(1)在温度不变的情况下,气球内的气体的压强p是它的体积V的反比例函数吗?写出它的解析式.(2)踩气球时,气球的体积会发生什么变化?根据第(1)小题的结果,此时气球内气体的压强会发生什么变化?这是根据反比例函数的那条性质?(3)当气球内气体的压强大到一定程度时,气球会爆炸吗?是0kpkkv为常数,体积变小压强会增大k>0,自变量v减小,则函数p逐渐增大气球会爆炸小明的妈妈在纳鞋底时,用锥子穿透鞋底,然后用拴有细绳的针顺着小孔眼从鞋底的这一面穿到另一面,为什么用锥子穿透鞋底,而不用小铁棍呢?压力F(N)等于压强p(Pa)乘以受力面积S(),即2mF=pS2、小明的妈妈给他做布鞋,纳鞋底时为什么用锥子?(2)小明的妈妈用的力一定时,锥子接触鞋底的面积怎样?根据第(1)小题的结果,鞋底上接触锥子的部位上受的压强怎样?如果不用锥子,而改用小铁棍,小铁棍接触鞋底的面积怎样?此时鞋底上接触部位上受的压强怎样?这是根据反比例函数的哪条性质?(1)当压力F一定时,压强p是受力面积S的反比例函数吗?写出它的解析式.(3)现在你明白了纳鞋底时,为什么要用锥子,而不用小铁棍吗?FPS是反比例函数锥子接触鞋底的面积小鞋底上接触锥子的部位上受的压强大小铁棍接触鞋底的面积大此时鞋底上接触部位上受的压强小减小受力面积,增大压强并且当k>0时,在第一、第三象限内,函数值随自变量取值的增大而减小;一个圆柱王国,住满了形形色色的圆柱,其中有一个底面积10m2,高为0.4m,膀大腰圆,威风八面,自己以粗壮为美,可近来却忧心忡忡,忽然变得自卑起来,探问何因?原来其他苗条的圆柱都在嘲笑它,说它太胖了,爱美的圆柱A既想让自己的空间优势不变(体积不变),又想让自己变瘦,想变成10m高,它使出了浑身的解数,也没实现自己的愿望.聪明的同学,你能帮圆柱A解除烦恼吗?3、圆柱的烦恼——怎么样减肥解:根据圆柱的体积公式:V=Sh(V圆柱的体积,S底面积,h高)。设高变为10m后,它的底面积变为xm2,根据变形前后体积不变,得10x0.4=10x,则x=0.4.因此,圆柱A要达到实现自己的愿望,只要让底面积变成0.4m2即可。4、你吃过拉面吗?你知道在做拉面的过程中渗透着数学知识吗?(1)体积为20cm3的面团做成拉面,面条的总长度y与面条粗细(横截面积)s有怎样的函数关系?(2)某家面馆的师傅手艺精湛,他拉的面条粗1mm2,面条总长是多少?市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?(2)公司决定把储存室的底面积S定为500m2,施工队施工时应该向下掘进多深?(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?探究二探究二解解::(1)(1)根据圆柱体的体积公式根据圆柱体的体积公式,,我们有我们有s×d=s×d=104变形得变形得即储存室的底面积即储存室的底面积SS是其深度是其深度dd的反比例函数的反比例函数..dS104市煤气公司要在地下修建一个容积为104m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?把把S=500S=500代入代入,,得得dS104d104500解得解得d=20d=20如果把储存室的底面积定为如果把储存室的底面积定为500500,,施工时应向地下掘进施工时应向地下掘进20m20m深深..m2(2)公司决定把储存室的底面积S定为500m2,施工队施工时应该向下掘进多深?解解::根据题意根据题意,,把把d=15d=15代入代入,,得得15104s解得解得S≈666.67S≈666.67当储存室的深为当储...