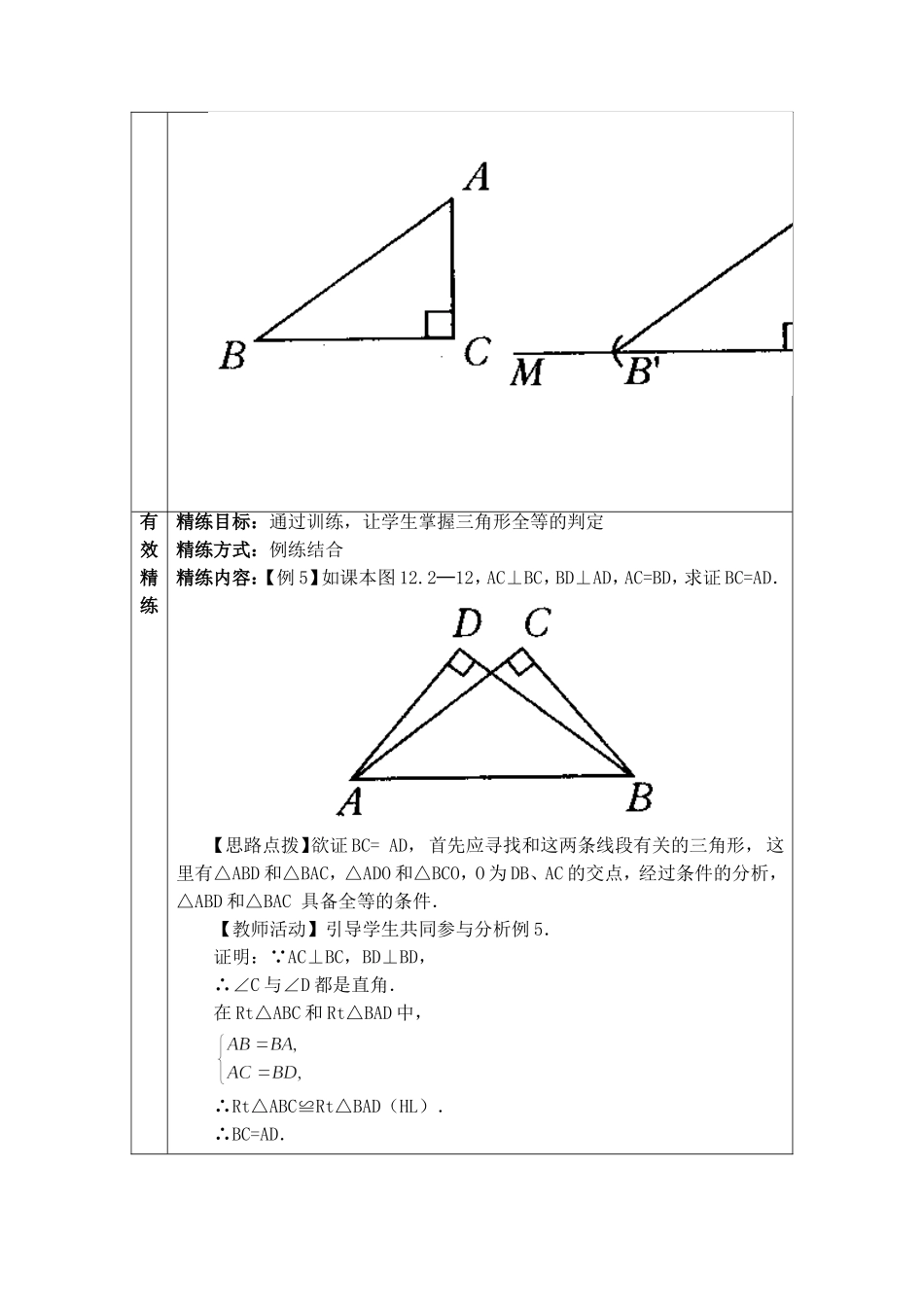
凤台四中专业性有效教学设计方案年级学科八年级数学课题12.2.4全等三角形的判定(四)时间2014.10.13主讲教师范广永教学课时1课时课型新授课教学目标目标:经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;掌握直角三角形全等的条件,并能运用其解决一些实际问题。重点:理解利用“斜边、直角边”来判定直角三角形全等的方法。难点:培养有条理的思考能力,正确使用“综合法”表达。有效导入导入目标:激发学习兴趣导入方式:问题导入导入内容:图1是两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形才能全等?【教师活动】操作投影仪,提出“问题探究”,组织学生讨论.【学生活动】小组讨论,发表意见:“由三角形全等条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.”有效精讲精讲目标:探索三角形全等的条件精讲方式:探索归纳式精讲内容:任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′,使B′C′=BC,A′B′=AB,把画好的Rt△A′B′C′剪下,放到Rt△ABC上,它们全等吗?【学生活动】画图分析,寻找规律.如下:规律:斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).有效精练精练目标:通过训练,让学生掌握三角形全等的判定精练方式:例练结合精练内容:【例5】如课本图12.2─12,AC⊥BC,BD⊥AD,AC=BD,求证BC=AD.【思路点拨】欲证BC=AD,首先应寻找和这两条线段有关的三角形,这里有△ABD和△BAC,△ADO和△BCO,O为DB、AC的交点,经过条件的分析,△ABD和△BAC具备全等的条件.【教师活动】引导学生共同参与分析例5.证明:∵AC⊥BC,BD⊥BD,∴∠C与∠D都是直角.在Rt△ABC和Rt△BAD中,∴Rt△ABC≌Rt△BAD(HL).∴BC=AD.【学生活动】参与教师分析,提出自己的见解.【评析】在证明两个直角三角形全等时,要防止学生使用“SSA”来证明.练习:1.课本练习1、22.判断题:(1)一个锐角和这个锐角的对边对应相等的两个直角三角形全等。()(2)一个锐角和锐角相邻的一直角边对应相等的两个直角三角形全等()(3)一个锐角与一斜边对应相等的两个直角三角形全等()(4)两直角边对应相等的两个直角三角形全等()(5)两边对应相等的两个直角三角形全等()(6)两锐角对应相等的两个直角三角形全等()(7)一个锐角与一边对应相等的两个直角三角形全等()(8)一直角边和斜边上的高对应相等的两个直角三角形全等()有效小结与作业设计小结作业:至此,我们有六种判定三角形全等的方法:1.全等三角形的定义2.边边边(SSS)3.边角边(SAS)4.角边角(ASA)5.角角边(AAS)6.HL(仅用在直角三角形中)课本习题6、7题教学后记