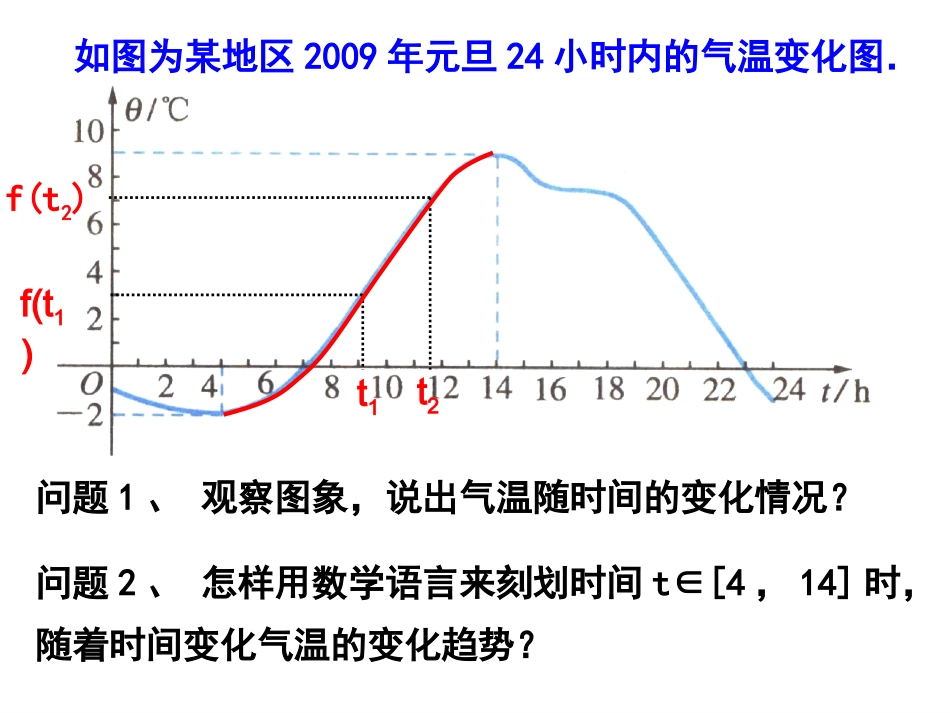
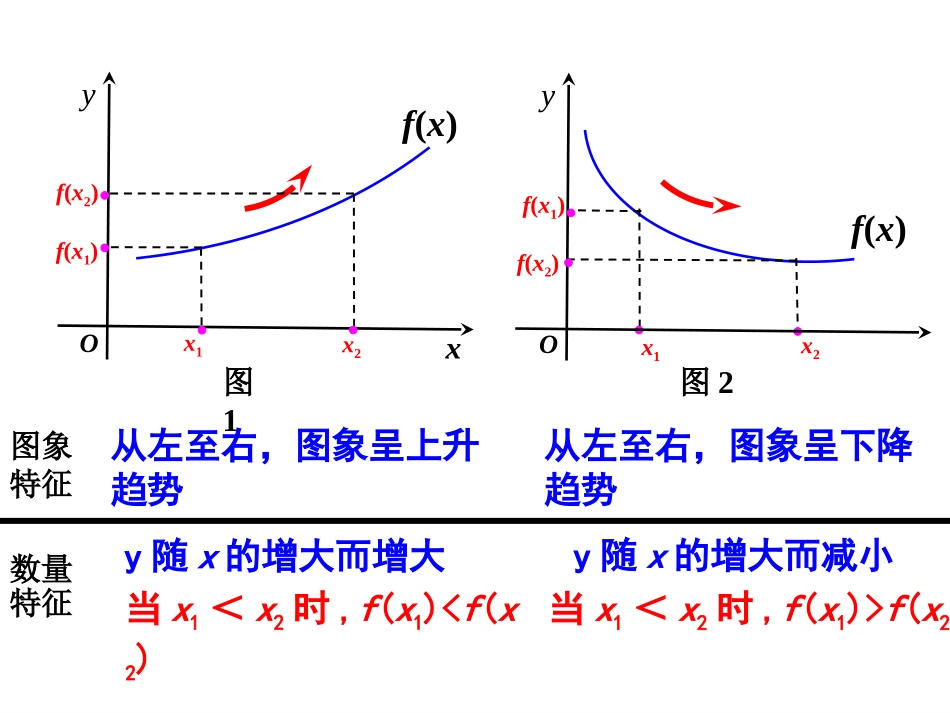
如图为某地区2009年元旦24小时内的气温变化图.问题2、怎样用数学语言来刻划时间t∈[4,14]时,随着时间变化气温的变化趋势?问题1、观察图象,说出气温随时间的变化情况?t1t2f(t1)f(t2)Oxyx1x2Oyx1x2从左至右,图象呈上升趋势从左至右,图象呈下降趋势y随x的增大而增大y随x的增大而减小当x1<x2时,f(x1)f(x2)图象特征数量特征f(x1)f(x2)f(x2)f(x1)图1图2f(x)f(x)如果对于函数y=f(x)定义域的某个子区间I内的任意两个自变量值x1、x2,当x1<x2时,都有f(x1)<f(x2),那么就说y=f(x)在区间I上是单调增函数,I称为y=f(x)的单调增区间.若函数y=f(x)在区间I上是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有(严格的)单调性.单调增区间和单调减区间统称为单调区间.如果对于函数y=f(x)定义域的某个子区间I内的任意两个自变量值x1、x2,当x1<x2时,都有f(x1)>f(x2),那么就说y=f(x)在区间I上是单调减函数,I称为y=f(x)的单调减区间.⑵在单调区间上,从左向右的方向看,增函数的图象只能呈现上升趋势,减函数的图象只能呈现下降趋势;⑴函数单调性是针对某个区间而言的,是一个局部性质;判断1:函数f(x)=x2在上是单调增函数;,xyo2yx⑶x1,x2取值的特征:任意性;有大小;同属于一个单调区间。判断2:若定义在R上的函数f(x)满足f(2)>f(1)则函数f(x)在R上是增函数;yxO12f(1)f(2)单调增区间:单调减区间:[4,14][0,4],[14,24]你能找出气温图中的单调区间吗?xyOxyOxyO22)(xxf32)(2xxxfxxf1)(说出所列举具体函数的单调区间,并判断函数在各区间上的单调性.练习1:下图是定义在区间[-5,5]上的函数y=f(x),根据图像说出函数的单调区间,以及每一单调区间上,它是增函数还是减函数?单调增区间是单调增区间是[-2,1),[3,5][-2,1),[3,5]答:函数答:函数y=f(x)y=f(x)的单调区间有的单调区间有[-5,-2),[-2,1),[1,3),[3,5],[-5,-2),[-2,1),[1,3),[3,5],其中单调减区间是其中单调减区间是[-5,-2),[1,3)[-5,-2),[1,3)例例11:证明函数:证明函数f(x)=3x+2f(x)=3x+2在在RR上是增函数。上是增函数。练习2:证明函数在区间(-∞,0)上是单调减函数.xxf1)(证明:设xx11、、xx22∈∈(-∞,0),且xx11<