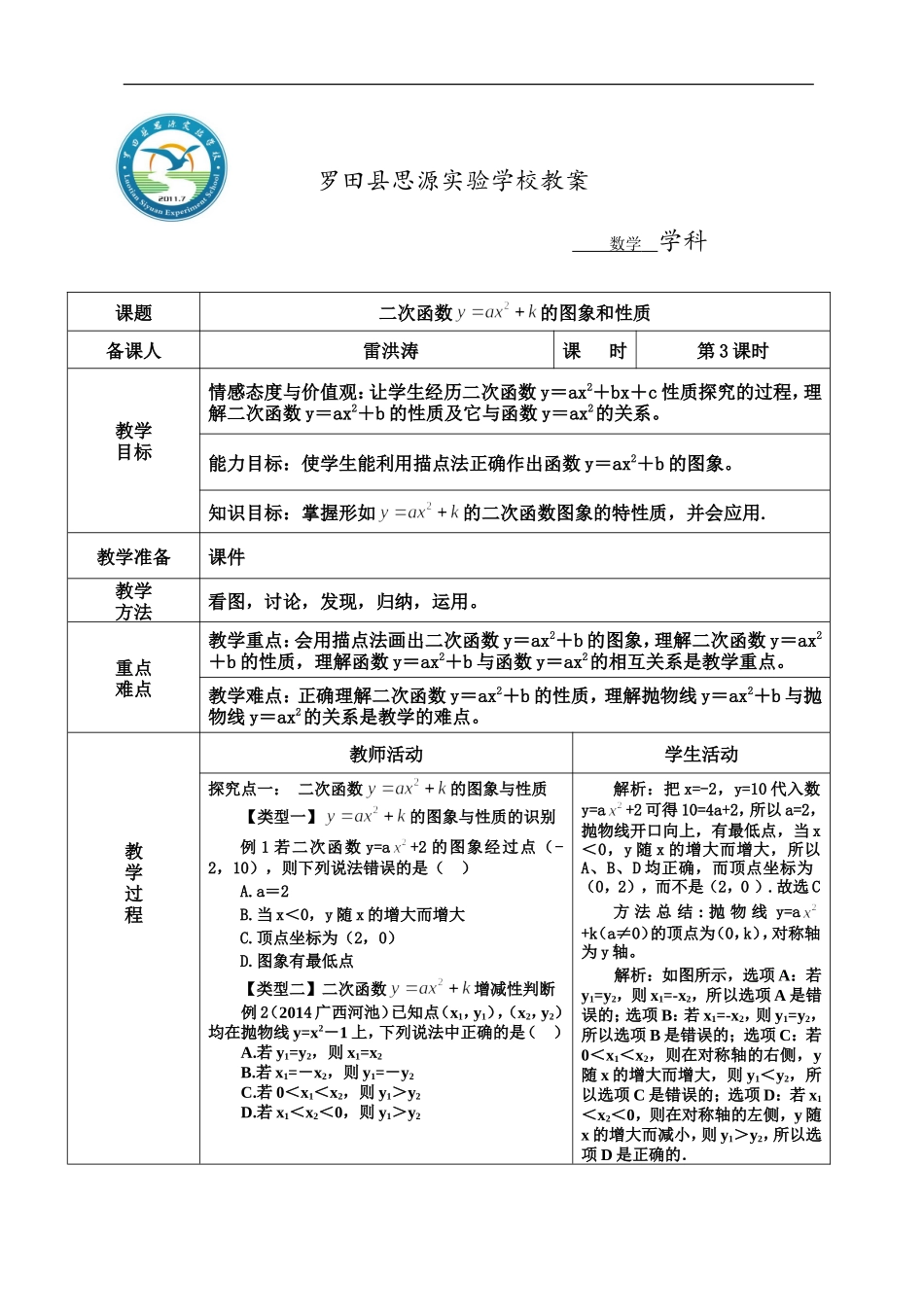
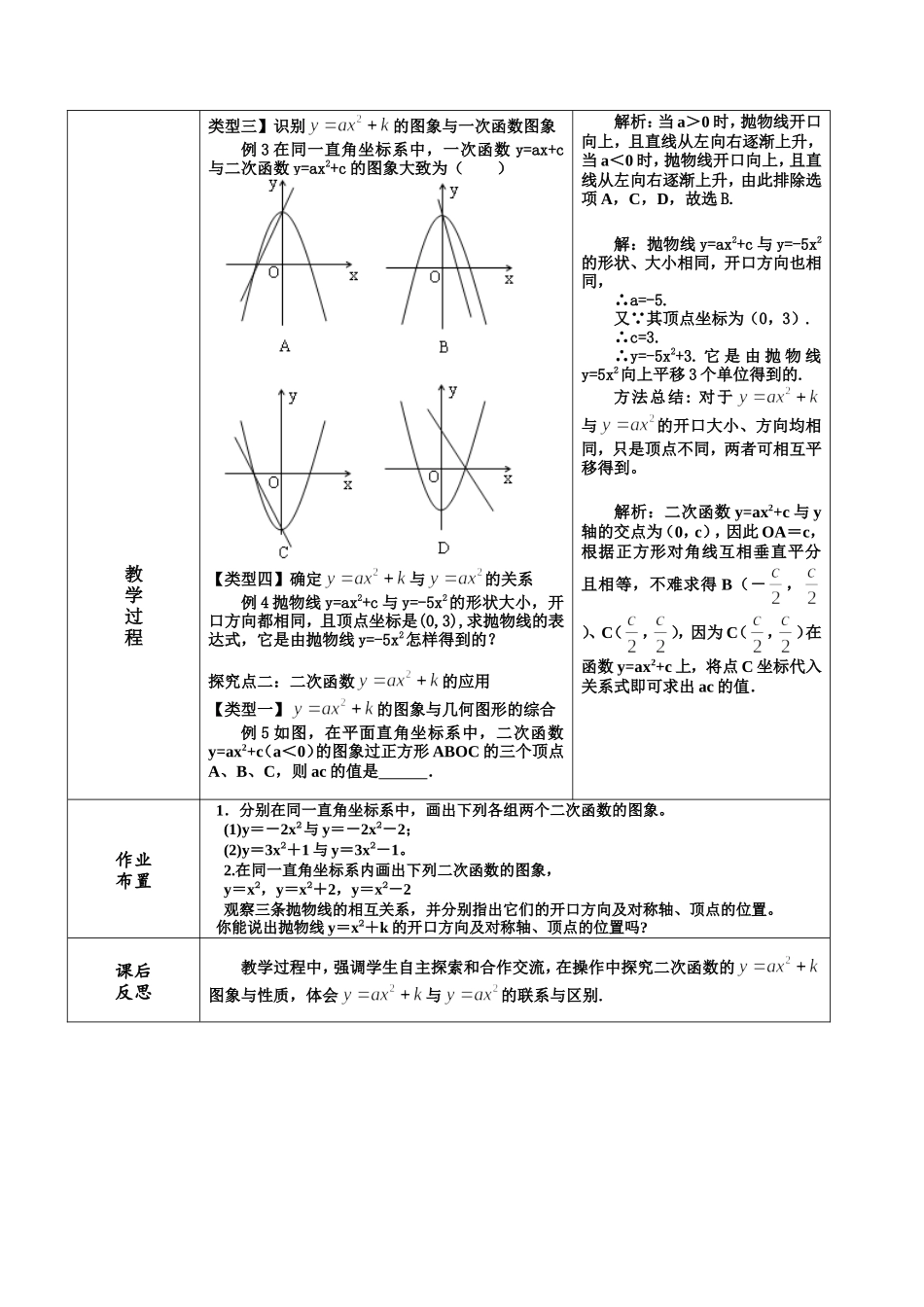
课题二次函数的图象和性质备课人雷洪涛课时第3课时教学目标情感态度与价值观:让学生经历二次函数y=ax2+bx+c性质探究的过程,理解二次函数y=ax2+b的性质及它与函数y=ax2的关系。能力目标:使学生能利用描点法正确作出函数y=ax2+b的图象。知识目标:掌握形如的二次函数图象的特性质,并会应用.教学准备课件教学方法看图,讨论,发现,归纳,运用。重点难点教学重点:会用描点法画出二次函数y=ax2+b的图象,理解二次函数y=ax2+b的性质,理解函数y=ax2+b与函数y=ax2的相互关系是教学重点。教学难点:正确理解二次函数y=ax2+b的性质,理解抛物线y=ax2+b与抛物线y=ax2的关系是教学的难点。教学过程教师活动学生活动探究点一:二次函数的图象与性质【类型一】的图象与性质的识别例1若二次函数y=a+2的图象经过点(-2,10),则下列说法错误的是()A.a=2B.当x<0,y随x的增大而增大C.顶点坐标为(2,0)D.图象有最低点【类型二】二次函数增减性判断例2(2014广西河池)已知点(x1,y1),(x2,y2)均在抛物线y=x2-1上,下列说法中正确的是()A.若y1=y2,则x1=x2B.若x1=-x2,则y1=-y2C.若0<x1<x2,则y1>y2D.若x1<x2<0,则y1>y2解析:把x=-2,y=10代入数y=a+2可得10=4a+2,所以a=2,抛物线开口向上,有最低点,当x<0,y随x的增大而增大,所以A、B、D均正确,而顶点坐标为(0,2),而不是(2,0).故选C方法总结:抛物线y=a+k(a≠0)的顶点为(0,k),对称轴为y轴。解析:如图所示,选项A:若y1=y2,则x1=-x2,所以选项A是错误的;选项B:若x1=-x2,则y1=y2,所以选项B是错误的;选项C:若0<x1<x2,则在对称轴的右侧,y随x的增大而增大,则y1<y2,所以选项C是错误的;选项D:若x1<x2<0,则在对称轴的左侧,y随x的增大而减小,则y1>y2,所以选项D是正确的.罗田县思源实验学校教案数学学科教学过程类型三】识别的图象与一次函数图象例3在同一直角坐标系中,一次函数y=ax+c与二次函数y=ax2+c的图象大致为()【类型四】确定与的关系例4抛物线y=ax2+c与y=-5x2的形状大小,开口方向都相同,且顶点坐标是(0,3),求抛物线的表达式,它是由抛物线y=-5x2怎样得到的?探究点二:二次函数的应用【类型一】的图象与几何图形的综合例5如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是.解析:当a>0时,抛物线开口向上,且直线从左向右逐渐上升,当a<0时,抛物线开口向上,且直线从左向右逐渐上升,由此排除选项A,C,D,故选B.解:抛物线y=ax2+c与y=-5x2的形状、大小相同,开口方向也相同,∴a=-5.又∵其顶点坐标为(0,3).∴c=3.∴y=-5x2+3.它是由抛物线y=5x2向上平移3个单位得到的.方法总结:对于与的开口大小、方向均相同,只是顶点不同,两者可相互平移得到。解析:二次函数y=ax2+c与y轴的交点为(0,c),因此OA=c,根据正方形对角线互相垂直平分且相等,不难求得B(-,)、C(,),因为C(,)在函数y=ax2+c上,将点C坐标代入关系式即可求出ac的值.作业布置1.分别在同一直角坐标系中,画出下列各组两个二次函数的图象。(1)y=-2x2与y=-2x2-2;(2)y=3x2+1与y=3x2-1。2.在同一直角坐标系内画出下列二次函数的图象,y=x2,y=x2+2,y=x2-2观察三条抛物线的相互关系,并分别指出它们的开口方向及对称轴、顶点的位置。你能说出抛物线y=x2+k的开口方向及对称轴、顶点的位置吗?课后反思教学过程中,强调学生自主探索和合作交流,在操作中探究二次函数的图象与性质,体会与的联系与区别.