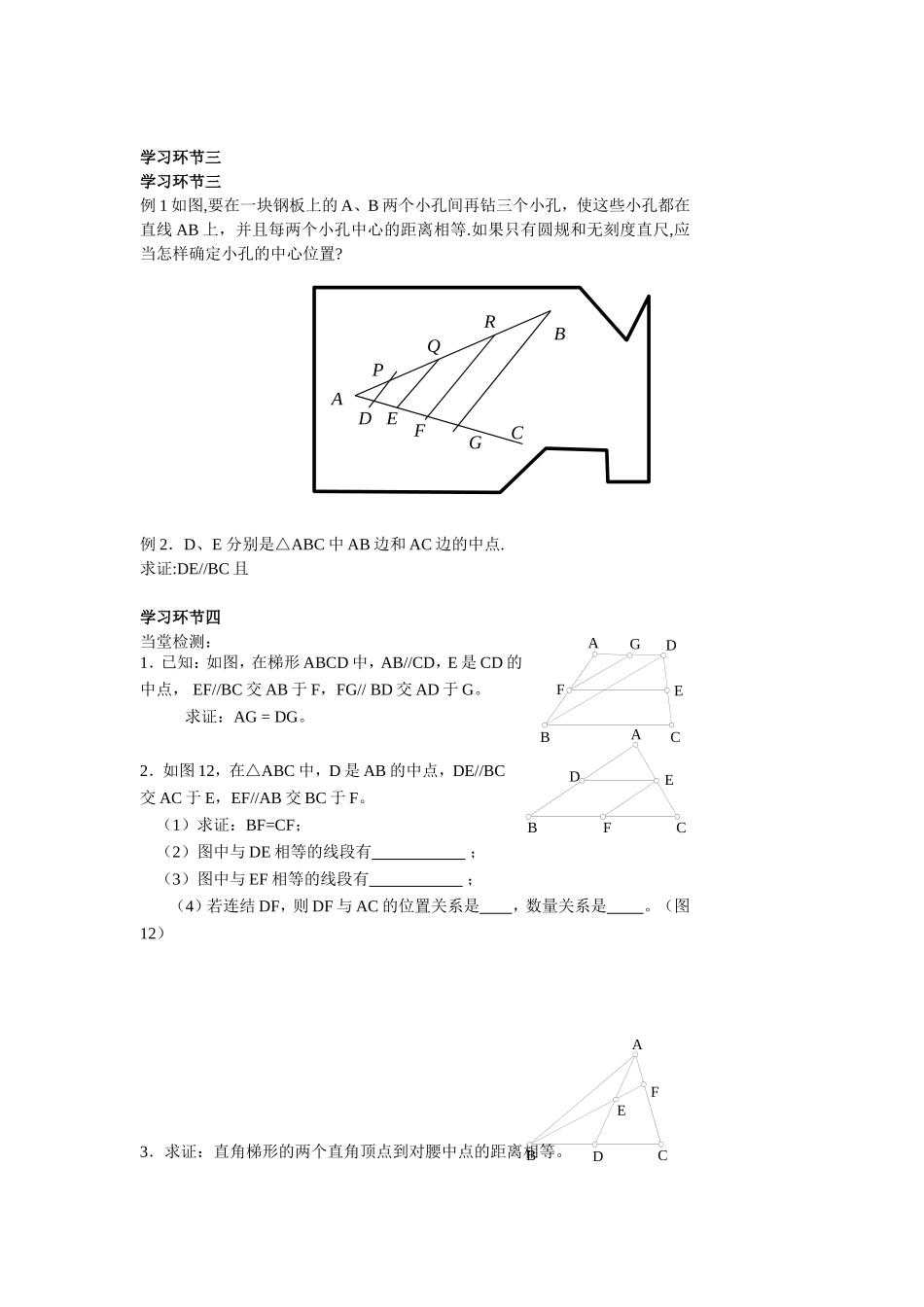
《1.1平行线分线段成比例定理》导学案3学习目标:1.使学生掌握平行线等分线段定理及推论.2.能够利用平行线等分线段定理任意等分一条已知线段,进一步培养学生的作图能力.学习重点:平行线等分线段定理学习难点:平行线等分线段定理学习环节一如果一组平行线在_________上挂得的线段相等,那么在________上截得的线段也相等.推论1:经过三角形一边_______与另一边平行的直线必____第三边.推论2:经过梯形一腰的_______,且与底______的直线,必_______另一腰.学习环节二判断题1、如图△ABC中点D、E三等分AB,DF∥EG∥BC,DF、EG分别交AC于点F、G,则点F、G三等分AC()2、四边形ABCD中,点M、N分别在AB、CD上若AM=BM、DN=CN则AD∥MN∥BC()3、一组平行线,任意相邻的两平行线间的距离都相等,则这组平行线能等分线段。()4、如图且AB=BC,那么AB=BC=DE=EF()CEBADGFABCDEF1l2l3l学习环节三学习环节三例1如图,要在一块钢板上的A、B两个小孔间再钻三个小孔,使这些小孔都在直线AB上,并且每两个小孔中心的距离相等.如果只有圆规和无刻度直尺,应当怎样确定小孔的中心位置?例2.D、E分别是△ABC中AB边和AC边的中点.求证:DE//BC且学习环节四当堂检测:1.已知:如图,在梯形ABCD中,AB//CD,E是CD的中点,EF//BC交AB于F,FG//BD交AD于G。求证:AG=DG。2.如图12,在△ABC中,D是AB的中点,DE//BC交AC于E,EF//AB交BC于F。(1)求证:BF=CF;(2)图中与DE相等的线段有;(3)图中与EF相等的线段有;(4)若连结DF,则DF与AC的位置关系是,数量关系是。(图12)3.求证:直角梯形的两个直角顶点到对腰中点的距离相等。BAPQRDEFGCABCDFEABCDEFABCDGFE4.已知:如图,AD是△ABC的中线,E是AD的中点,AE的延长线交AC于F。求证:FC=2AF。