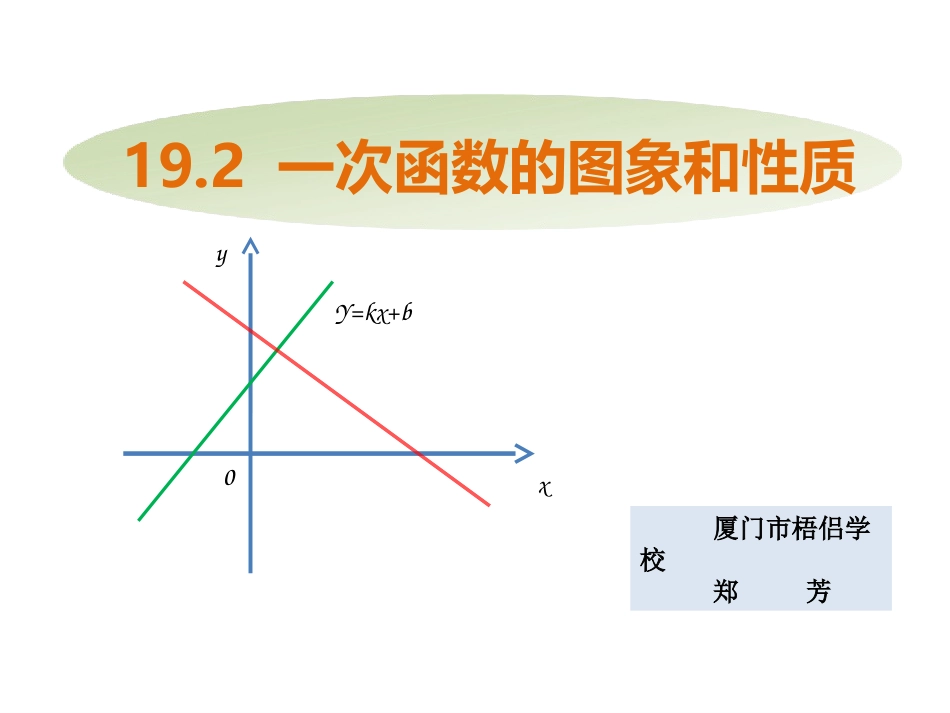
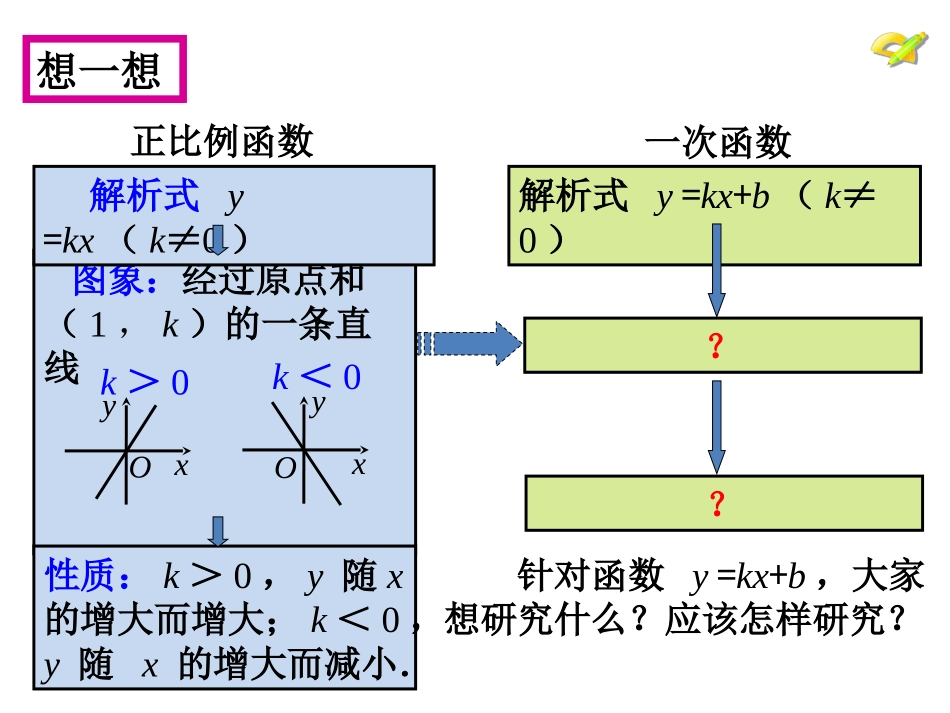
19.2一次函数的图象和性质厦门市梧侣学校郑芳Y=kx+bxy0联想旧知、导入新课1、正比例函数的解析式是什么?一次函数的解析式是什么?3、正比例函数图象有哪些性质?是怎样得到这些性质的?2、正比例函数与一次函数有何关系?图象:经过原点和(1,k)的一条直线想一想正比例函数解析式y=kx(k≠0)性质:k>0,y随x的增大而增大;k<0,y随x的增大而减小.一次函数解析式y=kx+b(k≠0)针对函数y=kx+b,大家想研究什么?应该怎样研究?xyOk>0k<0xyO??在同一直角坐标系中作出一次函数Y=2X、Y=2X+1、Y=2X-1的图象描点法:列表、描点、连线实践操作展示X…-2-1012…Y=2X+1…-3-1135…Y=2X-1…-5-3-113…这三个函数的图象形状都是一条,且倾斜度,即两直线的位置关系是。函数y=2x的图象经过原点,函数y=2x+1的图象与y轴交点,即它可以看作由直线y=2x向平移个单位长度而得到.相同(0,1)上10-2-112-3-4-534512345-1-2-3Y=2X+1Y=2X比较上面三个函数图像的相同点与不同点,填出你的观察结果。直线观察思考平行函数y=2x-1与y轴的交点为;它可以看作直线y=2x向平移个单位长度而得到;Y=2X-1(0,-1)下1xyy=xy=x+2y=x-2y30x2观察y=x、y=x+2、y=x-2的函数图象(0,2)(0,-2)猜想:对于一般的一次函数y=kx+b,它的图象形状是什么?它与直线y=kx有何关系?猜想:对于一般的一次函数y=kx+b,它的图象形状是什么?它与直线y=kx有何关系?一次函数y=kx+b(k≠0)的图象可以由直线y=kx平移︱b︳个单位长度得到(当b>0时,向上平移;当b<0时,向下平移)。一次函数y=kx+b(k≠0)的图象是一条直线,我们称它为直线y=kx+b。实践反馈,总结规律总结:一次函数的图像可由正比例函数的图象平移得到。归纳平移法则:(2)直线y=3x-2可由直线y=3x向平移个单位长度得到。巩固练习下2(1)正比例函数y=4x向平移个单位长度得到一次函数y=4x+3。上3两点法一次函数的图像是一条直线,在几何中直线是怎样确定的?由此能得到画一次函数图像的简便方法吗?(哪两个点?)合作探究两点确定一条直线画一次函数图象y用简便方法分别在坐标系中画出函数y=x+1,y=2x-1及y=-x+1,y=-2x-l的图象.合作探究xo11··y=-2x-ly=-x+1-1yxo11··y=2x-1y=x+1-1思考并讨论:一次函数解析式y=kx+b(k,b是常数,k≠0)中,k、b的正负对函数图象性质有什么影响?yxo11··y=2x-1y=-2x-ly=x+1y=-x+1思考:一次函数解析式y=kx+b(k,b是常数,k≠0)中,k、b的正负对函数图象性质有什么影响?-1合作探究当k>0时,直线从左向右,即y随x的增大而。当k<0时,直线从左向右,即y随x的增大而。当b>0时,直线交y的半轴;当b<0时,直线交y的半轴。上升增大下降减小正负归纳总结:k值决定直线上升、下降的趋势,b值决定直线与y轴交点的位置(0,b).k、b共同决定了图象所经过的象限。y=3x+2y=2x-5y=-2x-1y=-2x+3分别对应哪个函数图象?xyoxyoxyoxyo(k>0,b>0)(k>0,b<0)(k<0,b>0)(k<0,b<0)(1)直线y=2x-6的图象经过点(0,)与点(,0),图像经过_______象限,y随x的增大而。-63一三四增大巩固新知,拓展升华(2)一次函数y=kx+b,y随x的增大而减小,b>0,则它的图象经过第____________象限.一、二、四(3)已知一次函数y=(1-2k)x+k的函数值y随x的增大而增大,且图象经过一、二、三象限,则k的取值范围是__________.0k1/2﹤﹤巩固新知,拓展升华说说你的收获和体会。总结反思内化提升3、体验数形结合的思想与方法,从特殊到一般的思想与方法.1、画一次函数图象的方法:两点法、平移法2、一次函数的图象与性质。课后作业完成校本作业