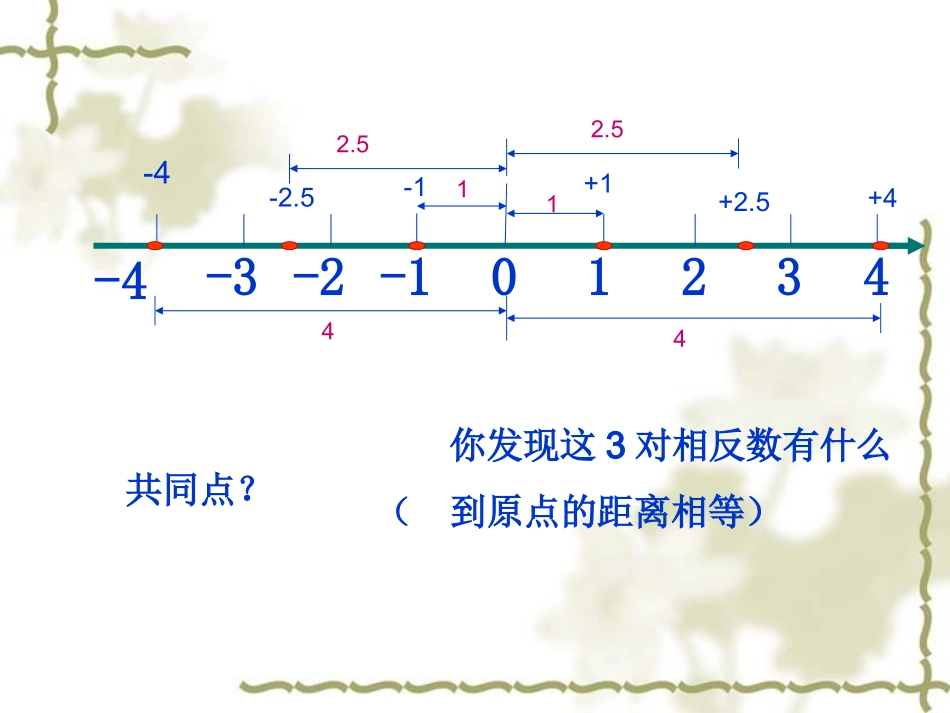
1.数轴的概念?其要素是什么?22、画一画:、画一画:+1+1和和-1-1,,+2.5+2.5和和--2.52.5,,+4+4和和-4-4把这些在数轴上标出把这些在数轴上标出..0123-1-2-3-44+1-1+2.5-2.5-4+42.52.51144你发现这3对相反数有什么共同点?(到原点的距离相等)问题1:两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(图1.2-5)。(1)它们的行驶路线的方向相同吗?。(2)它们行驶路程的距离(线段OA、OB的长度)相同吗?010AO-10B1010距离相同,(不管方向)方向不同,正负性思考:请举出生活中还有那些不注重考察其方向的实例?活动2:理解绝对值的概念绝对值概念:把在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作│a│.(1)│+3│=_____│+2/7│=_____│+8.5│=_____(2)|0|=_____(3)|-3|=_____,|-2/7|=______,|-8.5|=_______.绝对值的几何意义请试一试例1求下列各数的绝对值。-5,,0,-0.5,4.5,-6,+6,议一议:上述各数的绝对值与这些数本身有什么关系?绝对值的代数意义思考:(1)当a是正数时,|a|=____;(2)当a是负数时,|a|=__;(3)当a=0时,|a|=___。)0(0)0()0(||aaaaaaa-a0由此可以看出,不论有理数a取何值,它的绝对值总是正数或0(非负数).即对任意有理数a,总有|a|≥0.1、填空.(1)—3的符号是_________,绝对值是_________;(2)符号是“+”,绝对值是7的数是___________;(3)10.5的符号是_______,绝对值是________;(4)绝对值是5.1,符号是”-“的数是__________.—3+7+10.5-5.1例1求下列各数的绝对值:-15/2,+1/10,-4.75,10.5例2化简:1、│-(+1/2)│2、-│-4/3│练习3:(1)绝对值是12的数有几个?各是什么?(2)绝对值是0的数有几个?各是什么?(3)绝对值是-3的数是否存在?若存在,请说出来?回答问题:课本P25第4题必要:教材P25第2、3题。回顾与小结本节课里你学到了什么???(1)绝对值的几何意义及代数意义。(2)如何求一个数的绝对值。