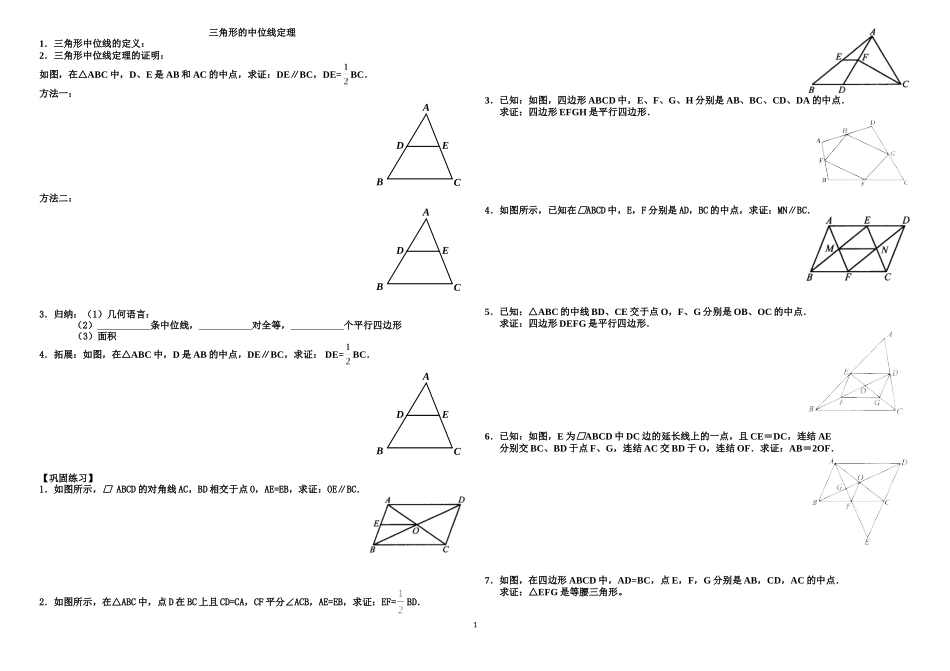
三角形的中位线定理1.三角形中位线的定义:2.三角形中位线定理的证明:如图,在△ABC中,D、E是AB和AC的中点,求证:DE∥BC,DE=BC.方法一:EDBCA方法二:EDBCA3.归纳:(1)几何语言:(2)条中位线,对全等,个平行四边形(3)面积4.拓展:如图,在△ABC中,D是AB的中点,DE∥BC,求证:DE=BC.EDBCA【巩固练习】1.如图所示,□ABCD的对角线AC,BD相交于点O,AE=EB,求证:OE∥BC.2.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD.3.已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.4.如图所示,已知在□ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.5.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.6.已知:如图,E为□ABCD中DC边的延长线上的一点,且CE=DC,连结AE分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.7.如图,在四边形ABCD中,AD=BC,点E,F,G分别是AB,CD,AC的中点.求证:△EFG是等腰三角形。1EFGDABC8.如图,在四边形中,点是线段上的任意一点(与不重合),分别是的中点.求证:四边形是平行四边形;9.如图,点E,F,G,H分别是CD,BC,AB,DA的中点.求证:四边形EFGH是平行四边形.10.已知:如图,DE是△ABC的中位线,AF是BC边上的中线,求证:DE与AF互相平分FEDBCA11.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于.求证:EF=FB.(多种方法)12.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.13.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点.求证:AF=FC(或证BE=3EF)14.已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.15.已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.16.已知:如图,在△ABC中,AB=AC,E是AB的中点,延长AB到D,使BD=AB.求证:CD=2CE.(多种方法)ABDCE2