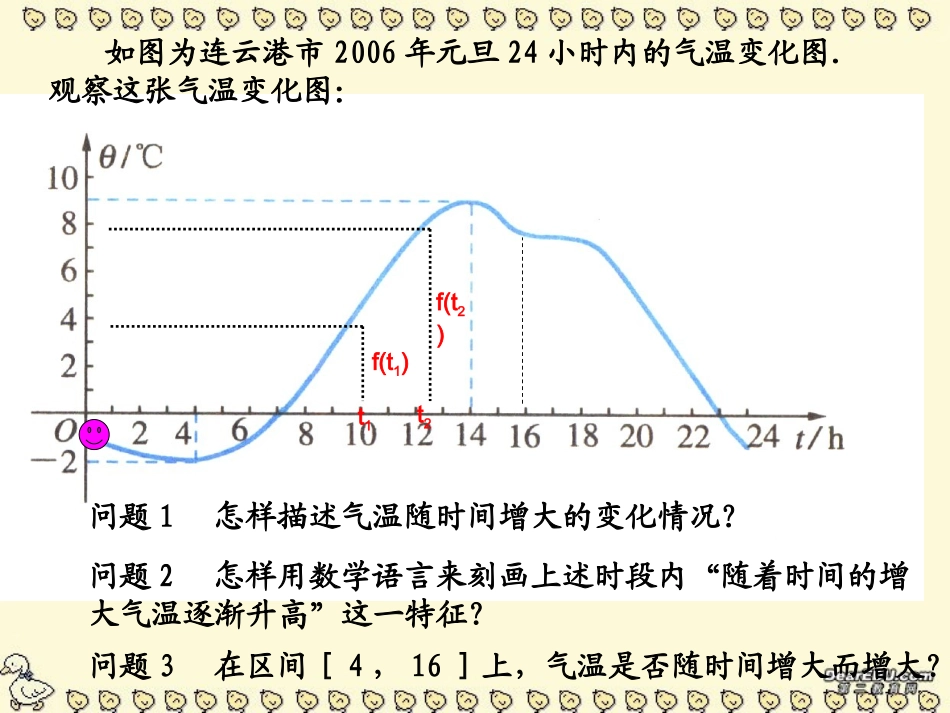
函数的单调性石榴高级中学高一数学组如图为连云港市2006年元旦24小时内的气温变化图.观察这张气温变化图:问题1怎样描述气温随时间增大的变化情况?问题3在区间[4,16]上,气温是否随时间增大而增大?问题2怎样用数学语言来刻画上述时段内“随着时间的增大气温逐渐升高”这一特征?t1t2f(t1)f(t2)f(x1)Oxy)x(fyx1x1f(x2),则称函数y=f(x)在区间I上是单调减函数,I称为y=f(x)的单调减区间。判断下列说法是否正确:(1)定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)是(-∞,+∞)上的单调增函数;(2)已知函数f(x)为(-∞,+∞)上的增函数,则有f(2)>f(1);(3)定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)不是(-∞,+∞)上的单调减函数;yxy=x-11-1oxx1yyoxyo2y=-x2+2221、单调增区间:(-∞,+∞)2、单调增区间:(-∞,0],单调减区间:[0,+∞)3、单调减区间:(-∞,0),(0,+∞)1、2、3、观察下列函数图象,写出单调区间.11-1-1函数的单调性是函数的局部性质证明:证明:对于区间(-∞,0)内任意x1,x2且x1<x2,121211()()fxfxxx1212xxxx1212,(,0)0xxxx12120xxxx求证:函数f(x)=在区间(-∞,0)上是单调增函数.11x121211()1,()1fxfxxx所以函数f(x)=在区间(-∞,0)上是单调增函数.11xf(x1)<f(x2)f(x1)-f(x2)<0区间取值作差变形判断符号给出结论问题讨论函数的单调性.1)(xxxf思考xyO-11通过本节课的研究,你对函数又多了哪些认识?你有什么收获?反思小结:课外作业:P43:1、2、4思考:1、已知函数y=f(x)在定义域R上是单调减函数,且f(a+1)>f(3-a),求实数a的取值范围。2、函数在[0,+)是增函数,你能确定字母的值吗?cbxxy2∞b