函数的单调性VIP免费

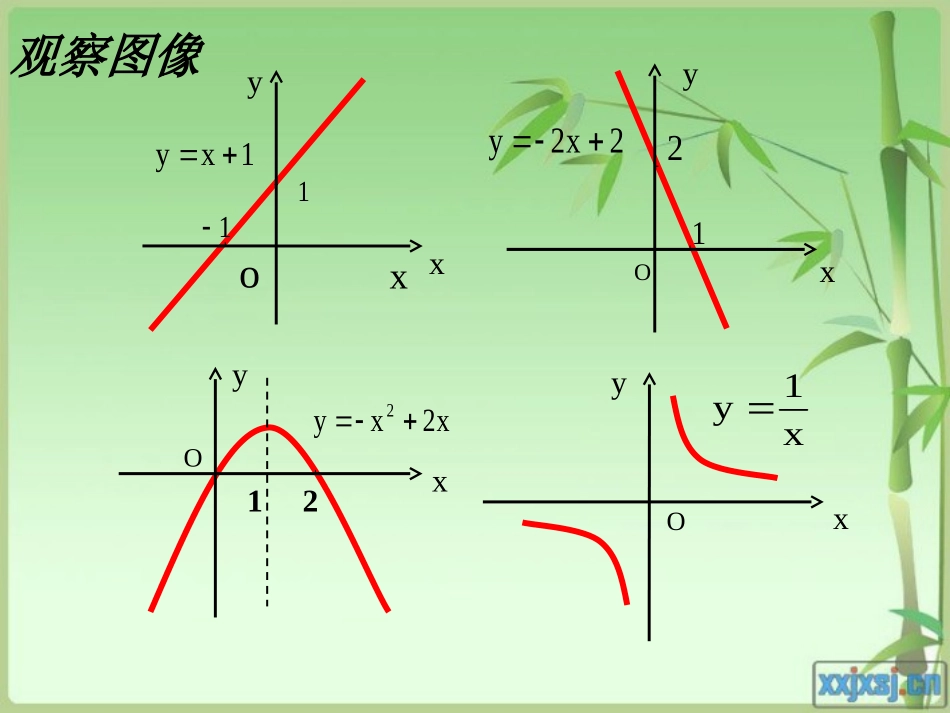
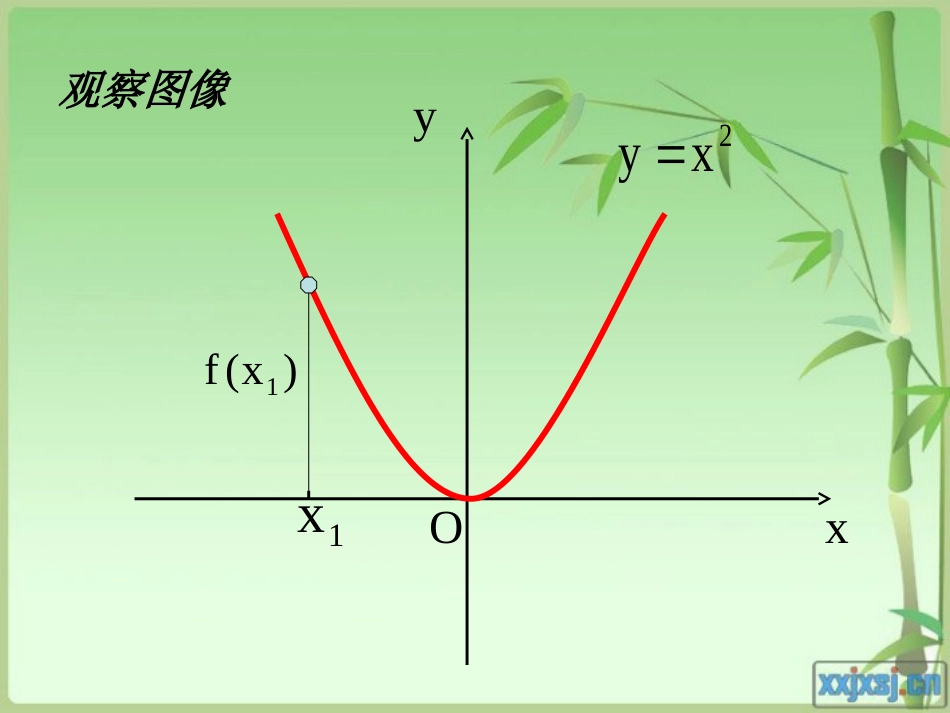
§3函数的单调性北师大版高中数学必修1灵璧县第一中学鄂化伟xy1xy11xy2x2y21Oxyx2xy221yOxx1yxoO观察图像Oxy1x)x(f12xy观察图像Oxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOxy1x)x(f12xyOx)x(f11xy2xyOxy)x(fy)x(f11x)x(f2)x(fyOxy)(1xf1x2x)x(f22x如何用x与f(x)来描述上升的图象？12,,xx在给定区间上任取12xx12f(x)f(x)函数f(x)在给定区间上为增加的。如何用x与f(x)来描述下降的图象？12,,xx在给定区间上任取12xx12f(x)f(x)函数f(x)在给定区间上为减少的。函数单调性的概念：1.如果对于属于这个区间任意两个数1212当xx时,都有f(x)f(x),称函数f(x)在这个区间上是递增的.2.如果对于属于这个区间任意两个数1212当xx时,都有f(x)f(x),称函数f(x)在这个区间上是递减的.一般地，如果函数y=f(x)在定义域内某个区间I上12x,x,12x,x,3.单调区间；如果函数y=f(x)在定义域内某个区间I上是增加的或是减少的,那么就说函数y=f(x)在区间I上具有单调性.单调增区间和单调减区间统称为单调区间.练习1：根据下列函数图象，写出其单调区间。y=x2y=x3y=x_1正确答案：增区间（-∞，0]，减区间[0，+∞）增区间（-∞，+∞）减区间（-∞，0），（0，+∞）2、定义在R上的函数满足，那么函数是R上的单调增函数吗？)(xf)1()2(ff)(xf概念深化概念深化请思考下列问题:2xy1、在R上是增函数还是减函数？1、函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质；注意：2、必须是对于区间D内的任意两个自变量x1，x2；当x1f(x2)分别是增函数和减函数.-5-1-2135f(x)解：函数y=f(x)的单调区间有[-5,-2)，[-2,1)，[1,3),[3,5]，其中y=f(x)在区间[-5,-2)，[1,3)上是减函数，在区间[-2,1)，[3,5]上是增函数。xyo例1、如图是定义在闭区间[-5，5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一单调区间上y=f(x)是增函数还是减函数例2、证明函数f(x)=3x+2在R上是增函数。证明：于是f(x1)-f(x2)<0,即f(x1)0)的单调性，并给出严格证明，你能求出该函数的值域吗？谢谢