二次函数的图像和性质(第2课时)VIP免费

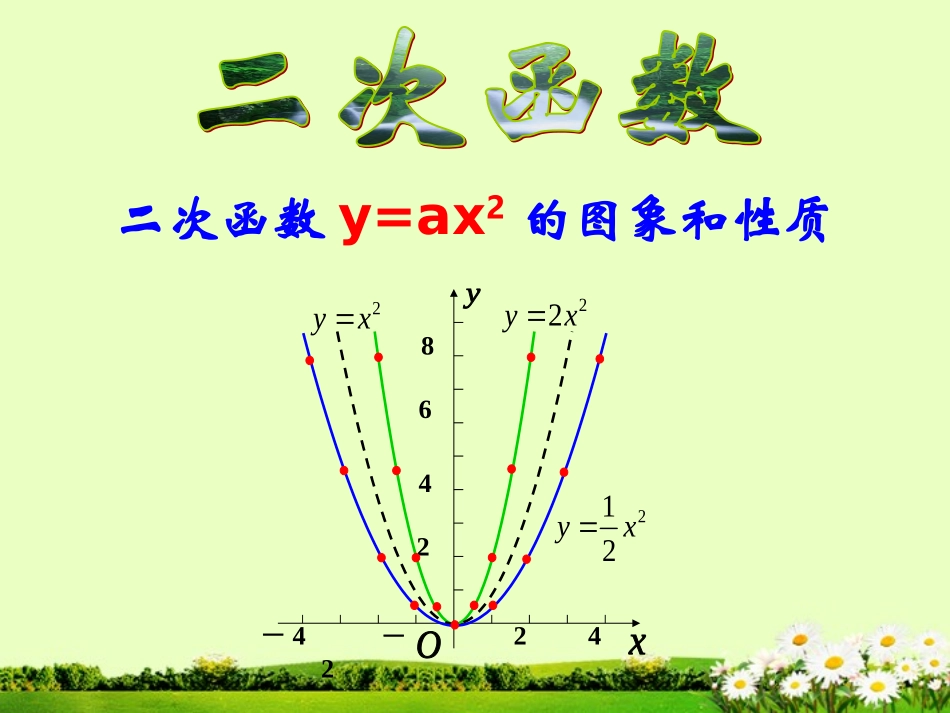
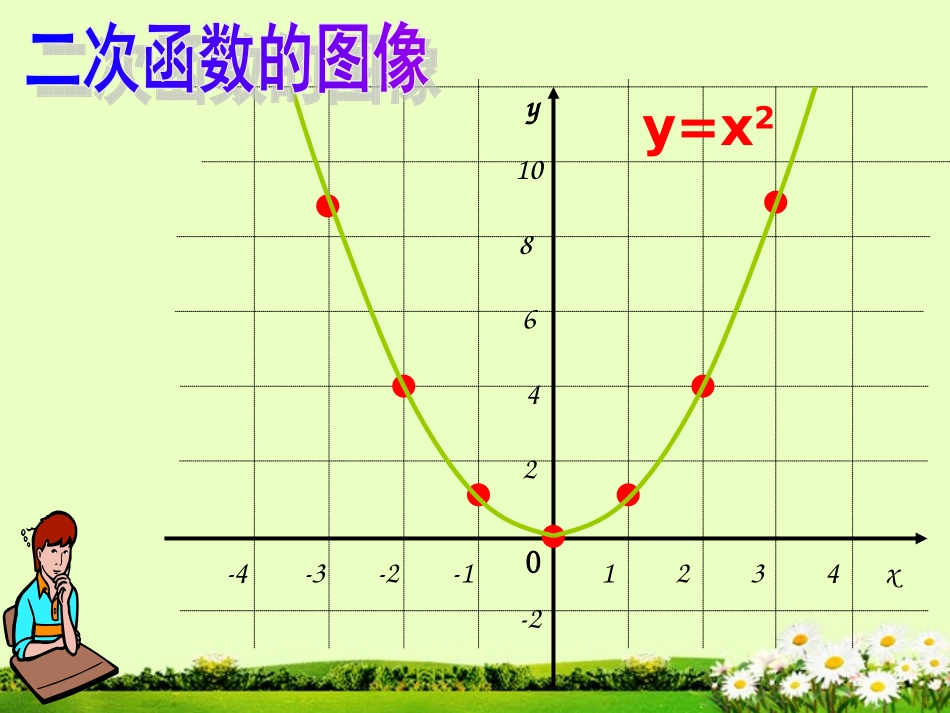
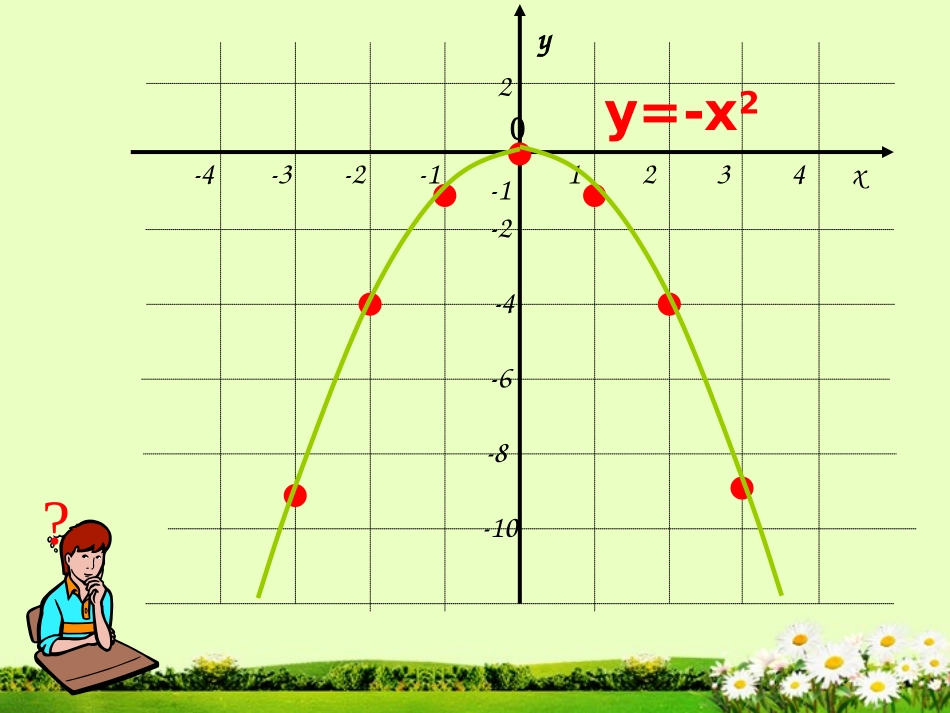
－222464－48212yx22yx2yx二次函数y=ax2的图象和性质xy0-4-3-2-11234108642-2y=x2xy0-4-3-2-11234-10-8-6-4-22-1?y=-x2在同一坐标系中作出函数y=x2和y=-x2的图象x0yy=x2y=-x2１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值二次函数y=ax2的性质抛物线顶点坐标对称轴位置开口方向增减性最值y=x2y=-x2（0，0）（0，0）y轴y轴在x轴的上方(除顶点外)在x轴的下方(除顶点外)向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.x…-4-3-2-101234…y=x2例1.在同一直角坐标系中画出函数y=x2和y=2x2的图像解:(1)列表12x…-2-1.5-1-0.500.511.52…y=2x28…20.500.524.58…4.58…20.500.524.58…4.512例1.在同一直角坐标系中画出函数y=x2和y=2x2的图像(2)描点(3)连线12345x12345678910yo-1-2-3-4-51222xy221xy12345x12345678910yo-1-2-3-4-5函数y=x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点?12不同点:共同点：开口向上;除顶点外,图像都在x轴上方开口大小不同;22xy221xyx…-4-3-2-101234…在同一直角坐标系中画出函数y=－x2和y=－2x2的图像解:(1)列表12x…-2-1.5-1-0.500.511.52…y=－2x2-8…-2-0.50-0.5-2-4.5-8…-4.5-8…-2-0.50-0.5-2-4.5-8…-4.512y=-x212345x-1-2-3-4-5-6-7-8-91yo-1-2-3-4-5-10(2)描点(3)连线22xy221xy12345x-1-2-3-4-5-6-7-8-91yo-1-2-3-4-5-10函数y=-x2,y=-2x2的图像与函数y=－x2(图中虚线图形)的图像相比,有什么共同点和不同点?12共同点:不同点:开口向下;除顶点外,图像都在x轴下方开口大小不同;22xy221xy12345x-1-2-3-4-5-6-7-8-91yo-1-2-3-4-5-1012345x12345678910yo-1-2-3-4-5一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.当a>0时,抛物线的开口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小当a<0时,抛物线的开口向上,顶点是抛物线的最高点,a越大,抛物线的开口越大;在同一坐标系内,抛物线y=ax2与抛物线y=－ax2是关于x轴对称的.a>0a<0221xy22xy2xy221xy22xy2xy|a|越大,抛物线的开口越小当a>0时，在对称轴的左侧，y随着x的增大而减小。当a>0时，在对称轴的右侧，y随着x的增大而增大。当a<0时，在对称轴的左侧，y随着x的增大而增大。当a<0时，在对称轴的右侧，y随着x的增大而减小。1.抛物线y=ax2的顶点是原点,对称轴是y轴.2.当a>0时，抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展；当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小；在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.当a<0时，在对称轴的左侧,y随着x的增大而增大；在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.二次函数y=ax2的性质二次函数y=ax2的性质1.已知抛物线y=ax2经过点A（-2，-8）.（1）求此抛物线的函数解析式；（2）判断点B（-1，-4）是否在此抛物线上.（3）求出此抛物线上纵坐标为-6的点的坐标.例题欣赏?解：（1）把（-2，-8）代入y=ax2,得-8=a(-2)2,解得a=-2,所求函数解析式为y=-2x2.（2）因为,所以点B（-1，-4）不在此抛物线上.2)1(24（3）由-6=-2x2,得x2=3,所以纵坐标为-6的点有两个，它们分别是3x)6,3()6,3(与2.填空:(1)抛物线y=2x2的顶点坐标是,对称轴是,在侧,y随着x的增大而增大；在侧,y随着x的增大而减小,当x=时,函数y的值最小,最小值是,抛物线y=2x2在x轴的方(除顶点外)（0，0）y轴对称轴的右对称轴的左00上(2)抛物线在x轴的方(除顶点外)在对称轴的左侧,y随着x的；在对称轴的右侧,y随着x的,当x=0时,函数y的值最大,最大值是,当x0时,y<0.232xy下增大而增大增大而减小0独立作业设正方形的边长为a,面积为S,试作出S随a的变化而变化的图象.x0yS=a2a>0已知y=(m+1)x是二次函数且其图象开口向上,求m的值和函数解析式m2+m解:依题意有:m+1>0①m2+m=2②解②得:m1=－2,m2=1由①得:m>－1∴m=1此时,二次函数为:y=2x21、已...