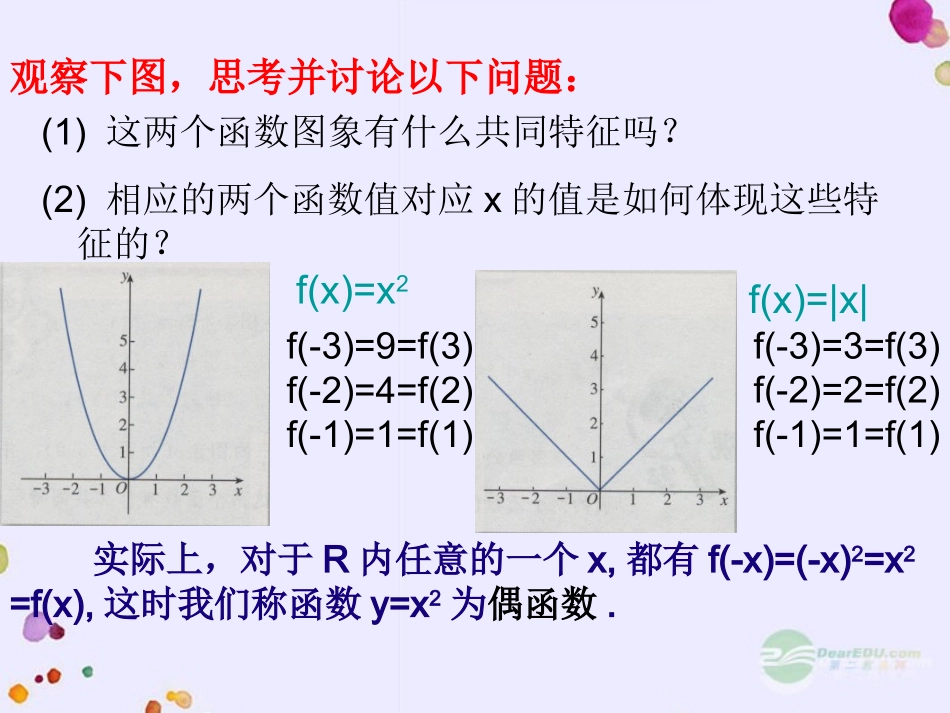
观察下图,思考并讨论以下问题:(1)这两个函数图象有什么共同特征吗?(2)相应的两个函数值对应x的值是如何体现这些特征的?f(-3)=9=f(3)f(-2)=4=f(2)f(-1)=1=f(1)f(-3)=3=f(3)f(-2)=2=f(2)f(-1)=1=f(1)f(x)=x2f(x)=|x|实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.1.偶函数P33一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.例如,函数都是偶函数,它们的图象分别如下图(1)、(2)所示.12)(,1)(22xxfxxf观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3)f(-2)=-2=-f(2)f(-1)=-1=-f(1)实际上,对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3)f(-2)=-1/2=-f(2)f(-1)=-1=-f(1)2.奇函数P35一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数.注意:(1)、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;(2)、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).(3)、奇、偶函数定义的逆命题也成立,即若f(x)为奇函数,则f(-x)=-f(x)成立.若f(x)为偶函数,则f(-x)=f(x)成立.(4)、若一个函数f(x)是奇函数,且当x=0时有定义,则:f(0)=0(5)、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.____,13)(:2mxmxxf则是奇函数若函数如0例1、(P35例5)判断下列函数的奇偶性:2541)()4(1)()3()()2()()1(xxfxxxfxxfxxf用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.]3,1[,)()4(1)()3(0)()2(5)()1(2xxxfxxfxfxf例2.判断下列函数的奇偶性:偶函数既奇又偶函数非奇非偶函数非奇非偶函数)(||)()5(2Raaxxxf当a=0时,偶函数,当a≠0时,非奇非偶函数3.奇偶函数图象的性质(1)、奇函数的图象关于原点对称.反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.(2)、偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.说明:奇偶函数图象的性质可用于:a、简化函数图象的画法.B、判断函数的奇偶性例3、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.xy0解:画法略相等例4、(1)当________时,f(x)=ax+b是奇函数,当________时,f(x)=ax+b是偶函数,(2)当________时,f(x)=ax2+bx+c是奇函数,当________时,f(x)=ax2+bx+c是偶函数,b=0a=0a=c=0b=0例5.(课本39页A6题)已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(1+x).画出函数f(x)的图象,并求出函数的解析式.例6.(课本39页B3题)已知函数f(x)是偶函数,而且在(0,+∞)上是减函数,判断f(x)在(-∞,0)上的是增函数还是减函数,并证明你的判断.例7.(作业本19页11题).,,,3)2(,2)1(,),,(1)(2的值求且是奇函数已知cbaffZcbacbxaxxf本课小结1、两个定义:对于f(x)定义域内的任意一个x,如果都有f(-x)=-f(x)f(x)为奇函数如果都有f(-x)=f(x)f(x)为偶函数2、两个性质:一个函数为奇函数它的图象关于原点对称一个函数为偶函数它的图象关于y轴对称3、判断函数的奇偶性:先看定义域,后验关系式。