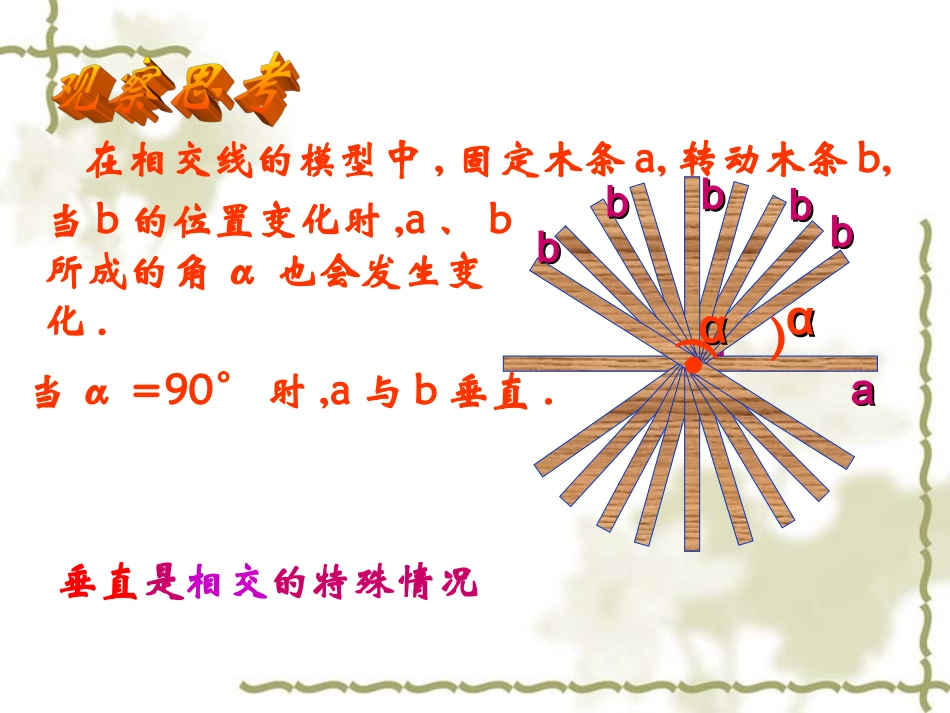
两条直线相交一般情况对顶角:相等邻补角:互补BACDO1234特殊情况在相交线的模型中,固定木条a,转动木条b,当α=90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.垂直是相交的特殊情况)ααaabbbbbbbbbb)αα1.1.垂直定义:垂直定义:当两条直线相交所成的四个角当两条直线相交所成的四个角中,有一个角是直角时,这两条直线中,有一个角是直角时,这两条直线互相垂互相垂直直,其中一条直线叫另一条直线的,其中一条直线叫另一条直线的垂线垂线,它,它们的交点叫们的交点叫垂足垂足..例如、如图,例如、如图,aa、、bb互相垂直互相垂直,O,O叫垂足叫垂足.a.a叫叫bb的垂线,的垂线,bb也叫也叫aa的垂线的垂线..baO从垂直的定义可知,判断两条直线互相垂直的关键:只要找到两条直线相交时四个交角中一个角是直角.一、垂直的定义一、垂直的定义ba用“⊥”和直线字母表示垂直用“⊥”和直线字母表示垂直Oα例如、如图,例如、如图,aa、、bb互相垂直互相垂直,,垂足为垂足为OO,则记为:,则记为:a⊥ba⊥b或或bb⊥⊥a,a,若要强调垂足,则记为若要强调垂足,则记为::a⊥b,a⊥b,垂足为垂足为O.O.2.2.垂直的表示:垂直的表示:读作“a垂直于b”FEMNO记作:MNEF,⊥垂足为O.或者MNEF⊥于OABOE记作:ABOE,⊥垂足为O.或者ABOE⊥于O垂直的定义的应用格式 ∠AOC=90°(已知),∴AB⊥CD(垂直的定义).如果直线AB、CD相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么AB⊥CD.这个推理过程可以写成: AB⊥CD(已知),∴∠AOC=90°(垂直的定义).如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:选择题:1、两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是(A)有两个角相等(B)有两对角相等(C)有三个角相等(D)有四对邻补角(C)2、下面四种判定两条直线的垂直的方法,正确的有()个(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直(3)两条直线相交,所成的四个角相等,这两条直线互相垂直(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直(A)4(B)3(C)2(D)1AACEBDO1∴∠∴∠EOB=90°EOB=90°((垂直的定义垂直的定义))∴∠∴∠EOD=EOD=∠∠EOB+EOB+∠∠BODBOD=90°+55°=145°=90°+55°=145°(解解:: AB⊥OEAB⊥OE(已知)(已知) ∠ ∠BOD=BOD=∠∠1=55°1=55°二、例题二、例题例1如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.(对顶角相等)(对顶角相等)ACEBDO∴∠∴∠EOB=90°EOB=90°((垂直的定义垂直的定义))∴∠∴∠COF=COF=∠∠CODCOD--∠∠DOF=180°DOF=180°--80°=10080°=100°°解解:: AB⊥OEAB⊥OE(已知)(已知)∴∠∴∠AOC=AOC=∠∠DOB=40°DOB=40°(对顶角相等)(对顶角相等)F ∠ ∠DOE=50°DOE=50°(已知)(已知)∴∠∴∠DOB=40DOB=40°°((互余的定义互余的定义))又 又 OBOB平分∠平分∠DOFDOF∴∠∴∠BOF=BOF=∠∠DOB=40°DOB=40°(角平分线定义)(角平分线定义)∴∠∴∠EOF=EOF=∠∠EOB+EOB+∠∠BOF=90°+40°=130°BOF=90°+40°=130°例2如图,直线AB、CD相交于点O,OE⊥AB于O,OB平分∠DOF,∠DOE=50°,求∠AOC、∠EOF、∠COF的度数.((邻补角定义邻补角定义))解:OEAB.⊥理由如下: ∠1=35°,∠2=55°(已知)且∠1+2+AOE=180°∠∠(平角的定义)例3、如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关系是CDABOE12∴∠AOE=180°-∠1-∠2=180°-35°-55°=90°∴OEAB(⊥垂直的定义)练习1:如图,直线AB,CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°,求∠BOE和∠AOC的度数.OFEDCBA∠BOE=65°,∠AOC=25°练习2:如图,ABC=90∠°,1=60∠°,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1=2,∠求∠ABO,BOD.∠ BOBO⊥AC⊥AC于于OO点点12ABCDO))(已知)(已知) ∠ ∠ABC=90ABC=90°()°()∠∠1=60°1=60°已知已知∴∠∴∠ABO=30°ABO=30°解:解:(已知)(已知)∴∠∴∠B...