正弦函数图象VIP免费

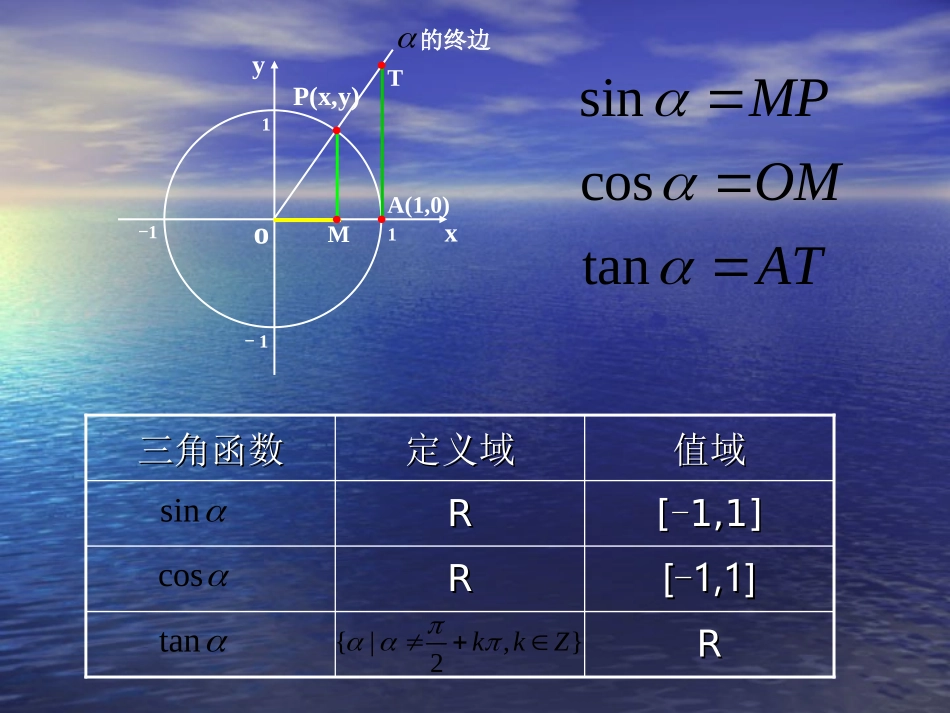
《正弦函数、余弦函数的图象》B(B)AXOY1-12πππ2π32xyoP(x,y)1-11-1M的终边A(1,0)TsincostanMPOMATRR[[--1,1]1,1]RR[[--1,1]1,1]RR值域值域定义域定义域三角函数三角函数sincostan{|,}2kkZ思考1：作函数图象最原始的方法是什么？思考2:用描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点？思考3：如何在直角坐标系中比较精确地描出这些点，并画出y=sinx在[0,2π]内的图象？三角函数三角函数线正弦函数余弦函数正切函数正弦线MPyxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！余弦线OM正切线AT由三角函数定义知我们可以用单位圆中的三角函数线刻画三角函数，能否用它来帮助作三角函数的图象呢？途径：利用单位圆中正弦、余弦线来解决。y=sinxx[0,2]O1Oyx33234352-11y=sinxxR终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ)()2(xfkxf描图：用光滑曲线将这些正弦线的终点连结起来利用图象平移AB为什么要将单位圆分成12等份？正弦函数的图象x6yo--12345-2-3-41yxo1-122322正弦曲线y=sinx()2,0y=sinxxRy=sinxx[0,2]再看一遍利用正弦线作函数2,0,sinxxy图象作法:oxy---11---1--21oA3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线(1)等分因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，…与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2xy---------1-12o46246正弦曲线yxo1-122322问：我们在作正弦函数y=sinxx[0,2∈π]的图象时，描出了12个点，但其中起关键作用的点是哪些？分别说出它们的坐标。(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)xsinx22302010-10再来一次,重点关注五个关键点,123,122,0(0,0),0xsinx22302010-10正弦函数的五个关键点x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同你能确定关键的五点吗？关系？正弦函数与余弦函数的关系xcosx23221O-1xy1010123220余弦函数的五个关键点y=cosx,x[0,2π]∈的简图1.函数2,0,sinxxy图象的几何作法....利用三角函数线作三角函数图象223xy11-----02-描点法:查三角函数表得三角函数值,描点,连线.)sin,(xx查表8660.0sin3y如:3x描点)8660.0,(3几何法：作三角函数线得三角函数值，描点)sin,(xx,连线作如:3x3的正弦线,MP平移定点),(MPxPM31Oxy几何法作图的关键是如何利用单位圆中角x的正弦线，巧妙地移动到直角坐标系内，从而确定对应的点(x,sinx).正弦函数正弦函数..余弦函数的图象余弦函数的图象2函数2,0,sinxxy图象的几何作法oxy---11---1--1oA作法:(1)等分3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线正弦函数正弦函数..余弦函数的图象和性质余弦函数的图象和性质正弦函数正弦函数..余弦函数的图象和性质余弦函数的图象和性质l1M1Q2M(1)等分作法：(2)作余弦线(3)竖立、平移(4)连线2Qyx---1--oxy---1121oA32326567342335611261P1M/1pyoxy---11---1--1o3232656734233561126正弦函数正弦函数..余弦函数的图象余弦函数的图象与x轴的交点)0,0()0,()0,2(图象的最高点图象的最低点)1,(23与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,...